11. Az erők természete
Az erőt úgy definiáltuk, hogy tömeg és a gyorsulás szorzata. Tehát ha egy tárgynak változik a sebessége, akkor ott valamilyen erő van. Na most definiálni bármit lehet bárhogyan, ahogy csak akarjuk. A matematika erről szól: definiálunk valamit és az azt leíró szabályokat, aztán játszunk vele, és kijön valami. Mindezt úgy, hogy nem tudjuk, hogy az adott dolog mit is jelent. Sőt a matematikában pont nem is kell azzal foglalkozni, hogy az adott dolognak van-e jelentése, csak játszani kell a betűkkel és az egyéb matematikai szimbólumokkal és annyi. A matematikában a szabályok és a definíciók pontosan igazak, ott nincs olyan, hogy „nagyjából” igaz.
A fizikában ezzel szemben a dolgoknak van jelentése, és semmi sem teljesen egzakt. Az erő nem csak annyi, amennyi mert úgy definiáltuk, hanem mert minden erőnek van valamilyen eredete. Pl. a Föld a gravitációjával húz minket lefelé, az elektromosan töltött részecskék vonzzák, illetve taszítják egymást. És ezek a dolgok nagyon is valóságosak.
A másik dolog pedig az, hogy minden elméletünk csak egy közelítés a valósághoz. Még nem találtuk meg a mindenség elméletét, amely teljesen pontosan leír mindent. Addig is minden (egyre bonyolultabb és bonyolultabb) modell, amit alkotunk egyre jobban közelíti, ami valóban történik. Azonban minden modellnek megvan a korlátja, amelyen túl azon adott modell egyre kevésbé lesz alkalmazható.
Számos erő, amit ismerünk ilyen közelítő modellből adódik. Ebben a részben a különféle erők fajtáiról lesz majd szó.
Közegellenállás
Amíg a gravitáció meglehetősen egyszerű törvény: csak 2 pont van benne, és pontosan kiszámolható, hogy mekkora vonzerő ébred köztük (erről a 6. részben volt bővebben szó). Addig a közegellenállás meglehetősen bonyolult. Például egy repülőgép esetén sok milliárd levegőmolekula kerülgeti a szárnyat, úgy hogy közben egymással is ütköznek. Nyilván nehéz lenne kiszámolni ezt pontosan.
Azonban ha csak egyszerűen a sebességet összevetjük a közegellenállási erővel, egy meglehetősen egyszerű összefüggést kapunk: A légellenállás által keltett erő a sebesség négyzetével arányos. Tehát 2-szer, 3-szor gyorsabban mozgó test esetén 4-szeres, 9-szeres a közegellenállási erő. A hétköznapi sebességek esetén ez a szabály a mérvadó.
Azonban, ha nagyon lassan mozgunk, akkor azt tapasztaljuk, hogy közegellenállás a sebességgel egyenesen arányos. Ennek az az oka, hogy az áramlás kis sebesség esetén lamináris, nagy sebesség esetén pedig örvényes, turbulens. Turbulens áramlás van akkor, amikor az autóval megyünk az úton. Lamináris leginkább akkor, amikor pl. a mézben mozgatjuk a kanalat. A másik véglet pedig a hangsebesség feletti mozgás. Ez esetben a hangnál gyorsabban mozgó repülő összenyomja maga előtt a levegőt. Azonban ez a túlnyomás nem tud előle elmenni, mert a nyomásváltozás csak hangsebességgel tud terjedni. Így a repülőnek ezt a nagy nyomású levegőfalat kell folyamatosan áttörnie. Ez nagyon erős hangot kelt, ez a hangrobbanás. Ez a nagy nyomású levegőből adódó „hullámellenállás” (wave drag) olyan nagy, hogy sokáig nem tudták átlépni a hangsebességet emiatt. Ezért is nevezték ezt sokáig a „hanghatárnak” (sound barrier). Manapság a repülőgépeknek már van akkora tolóereje, hogy semmi gondot nem jelent nekik a hangsebesség átlépése.
És ezekre a dolgokra nincs pontosan törvény, hogy mikor történik az átmenet laminárisból turbulensbe. Vagy hogy pontosan mennyi a hullámellenállás. Ezeket a dolgokat hagyományosan szélcsatornában mérik meg. A szuperszámítógépek és az összenyomható folyadékok szimulációjának a fejlődésével várhatóan háttérbe szorítja a szélcsatornákat a jövőben.
Ha a tárgy lassan halad a közegben, akkor a közeg könnyedén körüláramolja, az így kialakuló közegellenállás a sebességgel arányos. Ez a felületi súrlódás. Nagyobb sebességnél már örvények keletkeznek, ekkor a közegellenállás a sebesség négyzetével arányos. Szuperszonikus (hangnál gyorsabb) sebességnél a tárgy összenyomja maga előtt a levegőt, amely nem tud előre elmozdulni, mert a hangnál gyorsabban megyünk. Ez a nagy nyomású levegő mintegy kipárnázza a jármű elejét, effektíve megnövelve a felületét. Ekkor a közegellenállás a sokszorosára nő, ezt nevezték „hanghatárnak”. Amennyiben a hangsebességet jóval átlépjük ez a kipárnázottság megszűnik és a közegellenállás újra kisebb lesz, de továbbra is a sebesség négyzetével nő.
Súrlódás
Két szilárd test összedörzsölésekor súrlódási erő lép fel. Ennek az oka az, hogy mozgási energia fokozatosan áttevődik a dörzsölődő testekre, és hővé alakul. Azt figyelték meg, hogy ez az erő nagyjából egyenesen arányos a köztük lévő összenyomó erővel.
Megmérni úgy szokták, hogy egy lapra teszik a teszttárgyat, és addig emelik a lejtőt, amíg el nem kezd csúszni.
Egy lejtőn lévő testet a gravitáció lefelé húz. Ezt az erőt szét lehet bontani két merőleges összetevőre, úgy hogy az egyik összetevő a lejtőt nyomja ($F_n$), a másik pedig lejtő irányába mutat ($F_t$). Egy bizonyos szög felett a lejtőn lévő test megcsúszik. Ekkor a lejtővel párhuzamos és a lejtővel merőleges irányú erő hányadosa adja majd meg a súrlódási együtthatót. Ez a szám egyébként a lejtő szögének a tangense. Minél nagyobb szögnél indul meg a csúszás, annál jobb a tárgy tapadása, annál nagyobb súrlódási együttható.
A lejtő szögének a tangense lesz a súrlódási együttható. Azonban, amint elérjük a kritikus szöget nem kezd el azonnal és egyenletesen csúszni, hanem szakaszosan fog, ugyanis a súrlódási együttható mindenhol kicsit más és más lesz. Pl. azért, mert koszos lehet a lejtő.
Viszont azt is megfigyelték, hogyha lejtő rezeg, akkor a súrlódási együttható nagyban csökken. Nyilván azért, mert a rezgés nem engedi a felületek rendesen összetapadhassanak. De van egy másik véglet is. Ha pl. két fémfelületet nagyon simára csiszolunk, és nem hagyjuk, hogy a levegőben elrozsdásodjon, majd összenyomtuk, a két fémdarab összeragad. És nem fog elcsúszni egymáson, ha mégis, akkor azt erősen karcolva teszi. Ugyanis, hogyha nincs a két fém között szennyeződés vagy más idegen anyag, akkor a fémes kötés a két darab között minden további nélkül kialakulhat, és a két fémdarab összeragad és 1 fémdarab lesz belőle.
Molekuláris erők
Az atomok és molekulák között sokféle okból léphet fel erő. Például a vízmolekulák esetén a hidrogén felől pozitív a molekula, az oxigén felöl negatív. Az ilyen molekulát úgy nevezzük, hogy poláros. A vízmolekulák a hidrogénje vonzza a másik molekulában az oxigént. Amikor a víz megfagy, ennek megfelelően rendeződnek a vízmolekulák kristályrácsba.
Vannak nem poláros molekulák, mint pl. a szén-dioxid, vagy a metán, amelyben az atomok teljesen szimmetrikusan helyezkednek el. Ha egy poláros molekula, pl. víz közel kerül hozzájuk, mondjuk a pozitív végével, akkor az odavonzza a negatív elektronokat, az atommagot eltaszítja, így a semleges atom is poláros lesz.
Sőt két távolról semleges molekula se semleges annyira közelről. Az elektronok mozognak körülöttük, így szinte soha sem tökéletesen semlegesek. Ha az elektronok egy adott időpontban az atom egyik oldalán helyezkednek el, akkor az az atom ideiglenesen poláros lesz. És ez a polárosság képes arra, hogy a közelben lévő atomokban is átrendezze az elektronokat. Így két semleges atom is vonzhatja egymást.
Ezek a kölcsönhatások elég bonyolultak. A pontos leírásukhoz kvantummechanika szükséges. De általában elmondható, hogy az atomok és a molekulák távolról vonzzák egymást, közelről pedig taszítják.
Két atom között ébredő erő a távolság függvényében. Ha a két atom távol van egymástól, akkor gyenge vonzerő van közöttük, ha túl közel vannak egymáshoz, akkor taszítóerő lép fel köztük. Amikor a kettő egyensúlyban van, akkor mondjuk azt, hogy a két atom összeér.
Ez a vonzerő a távolság hetedik hatványával fordítottan arányos. Közelről viszont erős taszítás lép fel. A kettő között van egy olyan pont, ahol a vonzó és a taszító erő kiegyenlíti egymást. Ez az a távolság, amely két atom között akkor van, amikor a két tárgy éppen csak összeér. Ha összenyomjuk őket, akkor egy picit közelebb kerülnek, ha széthúzzuk őket, akkor pedig eltávolodnak egymástól. Elég erős húzás esetén pedig két atom szét is válik.
Minden görbe vonal egyenesnek fog látszani, ha elég közelről nézzük. Ez igaz a fenti ábrára is. Amikor egy acélrúgót széthúzunk, a benne lévő sok-sok milliárd atom egy picit eltávolodik egymástól. És ez az icipici eltávolodás miatt lesz egy kis vonzerő, ami visszahúzza. Összenyomás esetén pedig lesz egy kis ellenkező taszító erő, amely vissza akarja állítani a távolságot. Mivel az elmozdulás kicsi, ezért az erő az elmozdulással egyenesen arányosnak tekinthető. Pontosan így működik a rúgó. Egy kis mértékben minden szilárd anyag rugalmas is.
Erőterek
Gravitációs mező
Két test vonzza egymást pusztán azért, mert tömege van. Ezt már a 6. részben kitárgyaltuk, ez az általános gravitáció törvénye. Ez az erő egyenesen arányos a testek tömegével és fordítottan arányos a távolságuk négyzetével.
Na most tegyük fel, hogy van egy testünk, és a közelébe valahová teszünk egy 1 kg-os teszttárgyat. Nyilván valamekkora gravitációs erő fog hatni erre a teszt tárgyra, és húzni fogja valamerre. Ez egy erővektor lesz, nagysága és iránya van. Ezután tegyük át a testet máshová. Ott azon a másik helyen egy más irányú és nagyságú erő fog hatni rá. Aztán tegyük egy harmadik és negyedik és így tovább helyre, és megadhatjuk mindegyik helyen, hogy arra a testre mekkora gravitációs erő fog hatni.
Most képzeljük el, hogy ezt az erő mérést a tér összes pontjában elvégeztük. Így minden pontban meg tudjuk mondani, hogy mekkora erővel húz a gravitáció, hogyha odatennénk az 1 kg-os teszttárgyat. Tehát minden ponthoz rendelhetünk egy vektort. Na ez az, amit úgy nevezünk, hogy gravitációs erőtér, vagy gravitációs mező. A mezőket tipikusan erővonalakkal szokták ábrázolni:

A gravitációs erőtér erővonalai. (forrás)
Majd egy picit később még lesz szó az erővonalakról.
A gravitációs mező mértékegysége N/kg (newton per kilogramm). Mert a gravitációs erőt N-ban mérjük a teszt részecskét pedig kg-ban. A kettőt el kell osztani egymással, hogy megkapjuk a mező erősségét. A N/kg a gyorsulás mértékegysége. 1Mivel a N = kg m/s². És ezt osztjuk kg-mal. Ezért a gravitációs mező erősségét úgy is szokták mondani, hogy a gravitációs gyorsulás. Ez a Földön tengerszinten kb. 9,81 N/kg. 100 km magasan már csak 9,5 N/kg. Még távolabb még kevesebb.
Elektromos mező
Az előzőhöz hasonló módon megmérhető az elektromos mező is. Az elektromos taszító erő a töltések nagyságával egyenesen arányos, a távolság négyzetével pedig fordítottan arányos. A töltésekből van pozitív, és van negatív. Így ott vonzerő és taszítóerő is egyaránt lehetséges.
Az erőt newtonban (N), a töltést pedig coulombban (C). A mértékegysége az elektromos mezőnek így N/C. Azaz, az elektromos mező megadja, hogy mekkora erő hatna 1 C töltésre az egyes pontokban.
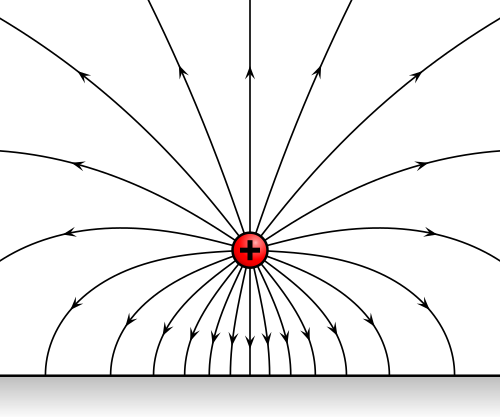
Az elektromos mező erővonalai a pozitív töltésből indulnak ki, és a hozzá képest negatívabb töltésű vezetőben végződnek. Esetünkben a talajban. Az elektromos erővonalak mindig merőlegesek a feltöltődött test felületére. (forrás, szerző, CC-BY-SA)
Mágneses mező
A harmadik mező, amiről szó lesz az a mágneses mező. A mágneses erő az az erő, amely észak-déli irányba forgatja az iránytűt. Az erő iránya adja meg, hogy milyen irányba fordul az iránytű. Az erő nagysága pedig azt adja meg, hogy mekkora nyomatékkal fordítja be az iránytűt irányba. A mágneses mező erősségének a mértékegysége a tesla (T).
A mágneses mező másik hatása pedig az, hogy mozgó elektromos töltésekre erővel hat. Ennek az erőnek az iránya merőleges a mező irányára és a mozgás sebességének az irányára is. Ez az ún. Lorentz-erő. Mivel ez az erő mindig merőlegesen hat az elektromos töltés mozgási irányára, ezért nem képes arra, hogy az elektromos töltés gyorsabban vagy lassabban mozogjon, csak a mozgás irányát változtatja meg.
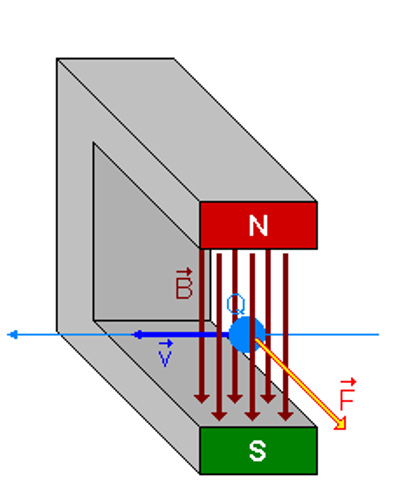
A Lorentz-erő merőleges a töltött részecske mozgási irányára és mágneses mező irányára is. (forrás, szerző 2drawn by Honina; edited by Head & Scdhönitzer , CC-BY-SA)
Ez az erő demonstrálható, hogyha egy régi katódsugárcsöves tévét bekapcsolunk és közelébe teszünk egy mágnest: a kép torzul, mert az elektronok a mágnes hatására eltérülnek.
Ennek a Lorentz-erőnek a nagysága egyenesen arányos a mágneses mező erősségével, a töltés mozgásának a sebességével, a töltés nagyságával és a mozgás iránya és a mező iránya által bezárt szög szinuszával. Tehát van két vektorunk, az erő és a sebesség. Ebből a kettőből csinálunk egy harmadikat úgy, hogy annak az iránya merőleges mind a kettőre, a nagysága pedig a 2 vektor szorzata, szorozva még a köztük bezárt szög szinuszával. Ez a két vektor ún. kereszt szorzata.
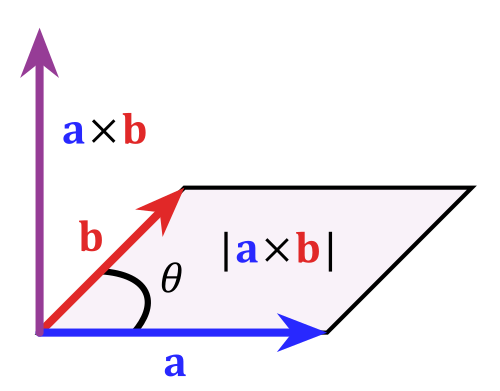
Két vektor keresztszorzatának a hosszát úgy is el lehet képzelni, hogy a két vektorból egy parallelogrammát formázunk. És annak a területét vesszük. Az iránya pedig merőleges mind a két vektorra. Hogy melyik irányba arra a következő hasonlat alkalmazható: képzeljük el, hogy az a szorzatvektor egy menetes szár, amin egy csavar van, az $\v a$ és a $\v b$ vektor pedig egy villáskulcsot jelképez. Ha ezt a villáskulcsot az $\v a$ irányából a $\v b$-be fordítod, akkor az irány az lesz, amerre a csavar mozog ezen a menetes száron. (forrás)
Ez azt jelenti, hogy ha a mágneses mező és az elektromos töltéssel rendelkező részecskék azonos irányba (vagy egymással pont ellenkező irányba) haladnak, akkor semmi erő nincs. Míg a legnagyobb akkor van, hogyha merőleges a kettő egymásra.
A Lorentz-erő okozza azt is, hogy két mágnes vonzza vagy taszítja egymást. Ugyanis egy rúdmágnes modellezhető egy elektromágnessel, amely lényegében egy dróttekercs, amelyben áram folyik. Azonban egy mágnes körül nem párhuzamosan futnak a mágneses erővonalak, hanem pólusok környékén szét vagy összetartanak. Ennek az eredménye az lesz, hogy a tekercsre ható Lorentz-erők nem fogják kiegyenlíteni egymást, hanem összességében húzni vagy tolni fogják tekercset.
A mágnes elképzelhető úgy, mint egy drótgyűrű, amelyben körbe-körbe folyik az áram. Azaz körbe-körbe mozognak a töltések. Ezen mozgó töltésekre Lorentz-erő hat. Amelyek összege, vagy másképpen mondva az eredője, a mágneses mező széttartása miatt a mágnes felé vagy az ellenkező irányba mutat.
Szuperpozíció elve
Ha több mágnes, vagy több elektromos töltés is van, akkor az általuk okozott erők egyszerűen összeadódnak, és együttesen mozgatják a töltött részecskéket. Ez a szuperpozíció elve a mezőkre.
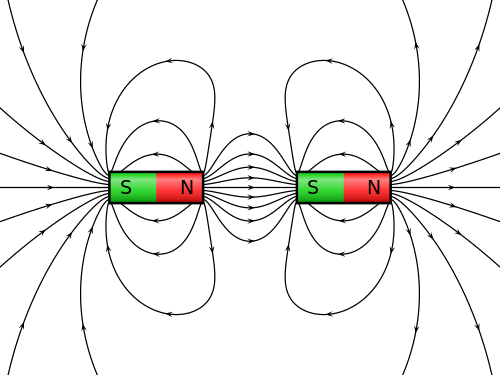
Két mágnes együttes mezőjét úgy kaphatjuk meg, hogy a két mágnes mezőjét összeadjuk. Minden pontban a két mágnes valamilyen erővel hat. Ha összeadjuk ez a két erőt, akkor megkapjuk a két mágnes együttes erejét. Ha ezt az összes pontban elvégezzük gondolatban, akkor összeadtuk a két mezőt. (forrás, szerző, CC-BY-SA)
Erővonalak
Megígértem, hogy később visszatérek az erővonalakra. Képzeljük el, hogy egy mágnes körül iránytűvel 3A madzagra lógatott fajtával, mert az 3 dimenzióban mér... megmérjük, hogy merre van észak. Azaz, hogy merre mutatnak a mágneses erővonalak. Aztán megyünk észak felé, pontosan arra amerre az iránytű mutat. Ha képzeletben rajzoljuk, ahogy megyünk, akkor azzal egy erővonalat rajzolunk. Az erővonalak hasznos segédeszközök, hogy elképzeljük az elektromos vagy gravitációs mezőt.
Mivel minden pontban csak 1 irányba mutat az erő, azért az erővonalak soha sem keresztezik egymást. Szintén érdekes dolog, ahol az erővonalak sűrűbbek, ott a mező is erősebb, ahol ritkábbak ott gyengébb. Az elektromos mező esetén az erővonalak, megállapodás szerint, a pozitív töltésű tárgyakból indulnak ki, és a negatív töltésű tárgyakban végződnek mindig. 4Legalább is a hozzá képest negatívabban. Ezzel szemben a mágneses mezőnek nincs forrása, ugyanis nincsenek mágneses töltések. Ennek a következménye az, hogy a mágneses mező erővonalai mindig önmagukba záródnak.
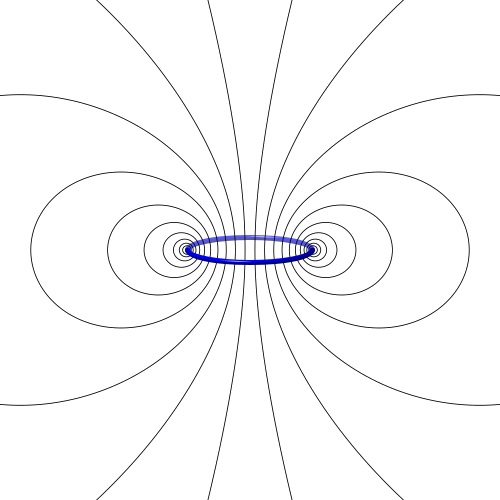
Egy drót gyűrűben körbefolyó áram mágneses mezője. Látható, hogy az erővonalak körbe folynak. Nincs kiinduló pontjuk, sem érkezési pontjuk. (forrás, szerző, CC-BY-SA)
Erőterek változása
A gravitációs, az elektromos és a mágneses mezők gyakran nem állandóak. Ha a mágnes vagy az elektromos töltés mozog, akkor az általa keltett mező is változik. Ez a változás azonban nem azonnali. Hanem a fény sebességével, kb. 300000 km/s sebességgel terjed. Ez azt jelenti, hogy az az elektromos mező, amit egy töltéstől 30 centire mérsz, nem a mostani állapotot tükrözi, hanem azt, ami 1 milliárdod másodperccel ezelőtt volt. Minél messzebb van valami, ez annál szembetűnőbb. Pl. ha itt a Földön megrángatjuk az elektromos mezőt, azaz rádióadást sugárzunk, a Marson ezt 20 perc múlva fogják érzékelni.
Majd később lesz szó arról, hogy az elektromos és a mágneses mező hogyan hat egymásra. Hogyan alkotják a közös elektromágneses mezőt, és majd azt is levezetjük, hogy hogyan terjedhetnek ebben a mezőben hullámok.
Nukleáris erők
Ezek azok az erők, amelyet már megemlítettem korábban: az erős kölcsönhatás, amely az atomokban a protonokat és a neutronokat tartja össze. Illetve a gyenge kölcsönhatás, amely részecskék bomlását teszi lehetővé.
Ahhoz, hogy jobban megértsük őket szükségünk van a kvantummechanikára, így majd később tárgyaljuk bővebben.
Fiktív erők
Nem minden erő származik közvetlenül elektromos töltésekből vagy atomokból. Vannak erők, amelyek máshonnét származnak. Például ha egy autóval gyorsítunk, akkor úgy érezzük, hogy egy erő a székbe nyom minket, illetve hogy a műszerfal tetején lévő bólogatós kutyát hátrafelé lerántja folyton valami. A körhintában is valamilyen erő húz minket kifelé. Ezek az erők csak azért vannak jelen, mert a koordináta-rendszer az időben változik. Az autóban azért érzünk egy hátrafelé ható erőt, amikor gyorsul az autó, mert az egész autó gyorsul, és gyorsítja a benne lévő tárgyakat is, és a látszólagos hátrafelé ható erő, az ennek az ellenereje. A körhintában pedig azért érzünk kifelé ható erőt, mert a körhinta a szerkezetéből adódóan nem engedi, hogy egyenes vonalban tovább repüljünk, hanem húz minket befelé, hogy a körpályán maradjunk. A kifelé húzó erő az ennek az ellenereje. Az egész a koordináta-rendszerből adódik. Az autóhoz rögzített koordináta-rendszerben nem látszik, hogy az autó gyorsulna, mert a koordináta-rendszer együtt mozog vele. A körhinta esetén is a koordináta-rendszer együtt forog körhintával, és a centripetális (befelé húzó) gyorsulás nem jelenik meg benne. Az ilyen koordináta-rendszer változásából adódó látszólagos erőket nevezzük fiktív erőknek.
Hogy mi a legérdekesebb ebben az egészben? Hogy ezek az erők pontosan egyenesen arányosak a tömeggel! Ez kicsit olyan, mint a gravitáció, nemde? Hiszen a gravitációs erő is a tömeggel arányos! Lehetséges, hogy a gravitáció is egy fiktív erő? A múlt század elején ez volt az alapgondolat, amely az általános relativitás megalkotásához vezetett. És ezen elmélet minden előrejelzése igaznak bizonyult. Később majd lesz szó az általános relativitásról is. Sokkal később...