15. Speciális relativitás
A sebesség relatív. Ahhoz, hogy ténylegesen mérjük a sebességet, kell valami, amihez viszonyítva mérjük azt. Az autóban az úthoz képest mérünk sebességet, a repülőgépen pedig a levegőhöz képest. Azonban ha semmi sem áll rendelkezésre, amihez képest sebességet mérhetnénk, akkor nem lehet sebességet mérni. Ha nincs viszonyítási pont kívül, akkor semmi módunk nincs arra, hogy megmérjük a sebességet. A sebesség nem egy belső önmagában értelmezhető tulajdonság. Ezért van az, hogy egy álló és egy mozgó környezetben ugyanaz a fizika van. Egy hangszigetelt, ablak nélküli, teljesen zötykölődésmentes vonatban ülve nem tudnánk megállapítani, hogy a jármű mozog-e vagy áll.
Amikor viszont felfedezték az elektromágnesességet. Rájöttek, hogy valami nincs rendben velük. Ugyanis olyan szabályok vannak az elektromágnesességben, amelyek attól függenek, hogy egy test mozog-e vagy áll. A 11. részben említettem a Lorentz-erőt, amely arról szól, hogy a mágneses mezőben egy mozgó elektromos töltésre erők hatnak a mozgás irányára merőlegesen. Aki nem hiszi mozgasson egy mágnest egy képcsöves tévé felé, hogy lássa, hogy hogyan torzul a kép. Ha viszont ugyanezt az elektromos töltés szemszögéből nézzük, akkor az saját magához képest egy helyben áll. és a mágnes mozog körülötte, ebben a helyzetben nincs erő, mert a részecske nem mozog. Akkor most van-e erő vagy nincsen erő? És ez ellentmondás, valami nincs ezzel rendben...
A vezetékben haladó áram (felfelé mozgó elektronok) mágneses mezőt keltenek, amely erővel hat a mozgásban lévő elektromos töltésre. Azonban, ha a töltés szemszögéből nézzük ezt, akkor ő saját magához képest áll, akkor most mihez képest kell a töltésnek mozognia, hogy hasson rá az erő?
Akkor a Maxwell egyenletek leírják az elektromágneses hullámokat. Ezek olyan egyenletek, amelyek leírják, hogy egy adott pontban az elektromos és a mágneses mező hogyan változik az adott pont közvetlen környezetében lévő elektromos illetve mágneses mező miatt. Sebességről nincs szó benne. Viszont az elektromágneses hullámok fénysebességgel terjednek, és ha a Maxwell egyenletek minden nézőpontból igazak, akkor az azt vonná maga után, hogy a fény minden nézőpontból fénysebességgel terjed. És ezzel sincs valami rendben. Ugyanis az út széléről nézve 130-cal száguldó autót egy 100-zal haladó autóból már csak 30-cal haladónak látjuk. Logikus következtetés lenne, hogyha az út széléről indított fénysugár irányában mozgunk egy gyors autóban, akkor a fénynek hozzánk képest lassabban kellene mozognia.
Vannak mechanikus hullámok is, amelyek terjednek valamilyen közegben. Pl. a hanghullámok a levegőben, a földrengéshullámok a földben terjednek. Jogos következtetés lenne, hogy akkor talán az elektromágneses hullámoknak is valamilyen terjedési közege, amelyhez képest mozog a fény. És akkor valóban lehetne arról beszélni, hogy lassabb a fény előre, hogyha ez a közeg szemből fúj. A hang sebessége tengerszinten kb. 340 méter másodpercenként. Ha 100 m/s sebességgel fújna a szél szemben, akkor ebből logikusan következik, hogy a hang előre csak 240 m/s-mal megy. Tehát feltételezték, hogy ez a paradox viselkedés feloldható lesz, hogyha az elektromágneses hullámoknak is van valamilyen vivőközege. Ezt a közeget annak idején úgy nevezték, hogy éter.
A fény sebességének állandósága
Na most nézzük meg, hogy mit kellene tapasztalnunk, akkor amikor fúj ez a bizonyos éterszél. Az egyik legismertebb ilyen kísérlet a Michelson-Morley kísérlet, melynek a sematikus leírása alább található:
Michelson kísérlet sematikus ábrája. Egy fényforrásból (pl. lézer) jön egy fénysugár, amely és féltükörre vetül. A fény fele átmegy a tükrön, a másik fele visszaverődik. A két fénysugár ezután visszaverődik egy rendes tükörről, majd a féltükörre visszaérve keverednek, és ennek a kevert sugárnak az egy része megérkezik a detektorba. Emiatt a keveredés miatt ez a kísérleti apparátus rendkívül érzékeny a fény sebességének a megváltozására, vagy a két karjának a hosszának a megváltozására. Ezért alkalmas a fény sebességének az esetleges változásának a megmérésére.
A dolog lényege, hogy egy fénysugarat egy féligáteresztő tükrön 2 részre bontunk. Majd a két egymásra merőleges irányban lévő tükörről visszaverődve újra egyesítjük. Na most a fény hullámokban terjed. A féligáteresztő tükörnél pedig találkozhat a két fénysugár úgy, hogy hullámhegy hullámheggyel, hullámvölgy hullámvölggyel, ekkor a két fénysugár erősíti egymást és fényerejük összeadódik. Illetve találkozhat úgy a két fénysugár, hogy hullámhegy hullámvölggyel, ekkor a két fénysugár kiüti egymást, és az eredmény sötétség lesz. Vagyis egy sötét vonal a detektorban. Ez elég érzékeny apparátus, hogy akár 1 mikronnyi (mm ezredrésze) eltérést is megérezzen a karok hosszának változásában. Ha pedig a fény sebessége változna valamelyik irányban, azt pedig még ennél is érzékenyebben tudná mérni.
Nézzük, hogy mit jelent ez betűkkel (már nem merem leírni, hogy „számokban”, mert olyat úgy sem látunk).
A fény egyszerre ér vissza akkor, amikor az apparátus áll. A szimuláció a képre kattintással indítható.
Legyen $L$ a két kar hossza. A fénysebesség szokásos jelölése $c$. Ekkor az út oda $L / c$. Vissza ugyanennyi, tehát $2L / c$ lesz az idő oda és vissza. Ez a kiindulási alapeset.
Most nézzük azt az esetet, amikor éterszél van. Tehát az apparátus mozog előre valamilyen $v$ nagyságú sebességgel az álló éterben, tehát van egy kis étermenetszél:
A fénynek nem kellene egyszerre visszaérnie, amikor az apparátus mozog. A szimuláció a képre kattintással indítható.
Először nézzük meg, hogy mennyi idő alatt ér vissza a fény a merőleges oldalon. Függőlegesen $L$ távolságot megy a tükörig, vízszintesen pedig $vt_1$-et, ahol $t_1$ az idő, míg oda nem ér. Az út hossza a Pitagorasz-tétel alapján: $\sqrt{L^2 + v^2 t_1^2}$, az idő, míg odaér pedig:
$$ t_1 = \frac{\sqrt{L^2 + v^2 t_1^2}}{c} $$
Ebből levezetjük $t_1$-et:
$$ t_1 = \frac{\sqrt{L^2 + v^2 t_1^2}}{c} \\ c t_1 = \sqrt{L^2 + v^2 t_1^2} \\ c^2 t_1^2 = L^2 + v^2 t_1^2 \\ c^2 t_1^2 - v^2 t_1^2 = L^2 \\ t_1^2 \left( c^2 - v^2 \right) = L^2 \\ t_1^2 = {L^2 \over c^2 - v^2 } \\ t_1 = {L \over \sqrt{c^2 - v^2} } \\ $$
Visszafelé, ugyanennyi idő, mert ugyanennyi utat tesz meg a fény, tehát a merőleges irányban a visszaérkezés időtartama (a $t_m$):
$$ t_m = {2 L \over \sqrt{c^2 - v^2} } \\ $$
Most nézzük meg, hogy menetirányban mennyi az idő:
Odafelé egyrészt meg kell tennie egy $L$ távolságot, illetve még egy $v t_1$ távolságot is, mert a $t_1$ idő alatt, amíg oda nem ér az apparátus előre mozog. Tehát a megtett út $L + v t_1$, és az idő míg odaér:
$$ t_1 = {L + v t_1 \over c} $$
Hozzuk ki ebből a $t_1$-et:
$$ t_1 = {L + v t_1 \over c} \\ c t_1 = L + v t_1 \\ c t_1 - v t_1 = L \\ t_1 \left(c - v\right) = L \\ t_1 = {L \over c - v} \\ $$
Ez volt az odaút. Most nézzük meg a visszautat. Itt is alapesetben $L$ távolságot kellene visszajönnie, de közben az apparátus megy előre, így $v t_2$-vel kevesebbet kell a fénynek mennie. $t_2$ az idő, míg vissza nem ér. A megtett út visszafelé így $L - v t_2$. Az ehhez szükséges idő:
$$ t_2 = {L - v t_2 \over c} \\ c t_2 = L - v t_2 \\ c t_2 + v t_2 = L \\ t_2 \left(c + v\right) = L \\ t_2 = {L \over c + v} \\ $$
Azaz a menetirányban történő visszaérkezéshez szükséges idő, ha ezt az előző kettőt összevonjuk:
$$ t_p = {L \over c - v} + {L \over c + v} = \\ {L (c + v + c - v) \over c^2 - v^2} = \\ {2 L c \over c^2 - v^2} \label{eq:paralleldir} $$
Most nézzük meg, hogy a menetirányban és a menetirányra merőlegesen a visszaérkezéshez szükséges idő hogyan aránylik egymással:
$$ {t_p \over t_m} = {{2 L c \over c^2 - v^2} \over {2 L \over \sqrt{c^2 - v^2} }} = \\ {2 L c \over c^2 - v^2} {\sqrt{c^2 - v^2} \over 2 L} = \\ {c \over \sqrt{c^2 - v^2}} = \\ {1 \over \sqrt{1 - v^2/c^2}}\\ $$
A kettő nyilvánvalóan nem egyenlő, hanem függ a sebességtől. Ezt az arányt $\gamma$ jellel szokták jelölni. Egyébként ez az arány nagyon kicsi. A fény sebessége kerekítve 300 000 000 m/s. Ha veszünk egy műholdat, ami 8000 m/s sebességgel megy, akkor fenti képletbe behelyettesítve azt kapjuk, hogy: a szám 1,000000000355555 lesz. Gyakorlatilag 1. De ha már olyan nagy sebességekről van szó, mint mondjuk 150000 km/s, azaz a fénysebesség fele, akkor már ez a szám 1,15. 290000 km/s esetén már 3,9. Végül a fénysebességhez közeledve gyorsan tart majd a végtelenhez. Ennek a hányadosnak a pontos megmérése lehetővé teszi az éterszél sebességének a meghatározását.
A múlt században készítettek számos ötletes kísérleti berendezést, amelynek a segítségével az éterszelet nagyon pontosan meg lehet mérni. Ma már ott tartunk van olyan pontos berendezés, amely már azt is kimutatná, hogyha felemeljük és járunk vele az asztal körül egy kört. Azonban ez mind hiábavaló volt, mert nem sikerült semmilyen éterszelet sem kimutatni. Nincs éterszél.
Viszont más megfigyelések meg arra utalnak, hogy van. Ilyen például az aberrációnak nevezett jelenség. Ezt leginkább a következőképpen lehet elképzelni. Képzeljük el, hogy esik az eső. Nincs szél, tehát a cseppek függőlegesen esnek lefelé. Na most ha egy kocsival elindulunk előre, és kinézzünk az ablakon, azt látjuk, hogy az esőcseppek nem függőlegesen esnek, hanem menetiránnyal ellenkezőleg hátrafelé ferdén. Ez szükségszerű következménye annak, hogy a kocsiból nézve hátrafelé megy a tárgy, így az esőcseppek is. Ha azt szeretnénk, hogy az esőcseppek átessenek egy csövön, akkor álló helyzetben függőlegesen kell tartanunk azt a csövet, mert függőlegesen esnek. De a mozgó autóban már nem, ott menetirányban kicsit előre kell döntenünk a csövet, hogy átessenek rajta a cseppek. És pontosan ezt kell csinálni akkor is, amikor távcsővel egy csillagot figyelünk meg. Ha ugyanis a mozgás miatt más irányból jön a fény, akkor az adott csillag más irányban fog látszani. A Föld ugyanis nagy sebességgel kering a Nap körül (kb. 30 km/s-mal), és ez a hatás mérhető.
Az aberráció jelensége. Ahhoz, hogy az esőcseppek átessenek a csövön megfelelő szögben kell azt tartani. A szimuláció a képre kattintással indítható. Látható, hogy a mozgó csövet ferdén kell tartani, hogy átessen rajta az esőcsepp. Ugyanezt megfigyelték fény esetén is. Amikor egy csillagot megfigyelünk, egy picit a Föld menetirányába kell fordítani a távcsövet, hogy lássuk a csillagot.
Tehát ez viszont arra utal, hogy van éterszél. Így a két mérés egymásnak ellent mond.
Természetesen valaki ilyenkor még mindig mondhatja, hogy mi van, hogyha a fény nem is hullám, hanem olyan, mint az esőcseppek, tehát kis részecskék? Akkor is van aberráció és fenti Michelson kísérlet sikertelenségét is magyarázná, hiszen a fényforrás is a kísérleti apparátussal egyszerre mozog, így a fény vele együtt mozog, és jó, hogy nem észlelünk változást a mozgó állapotban. Viszont ha az így lenne, akkor egyes csillagokból más és más sebességgel jönne a fény attól függően, hogy az közeledik-e vagy távolodik. Ez kettős csillagoknál érdekes problémákat okozhat: amikor a csillag közeledik, akkor gyorsabb fény jönne, amikor távolodik, akkor lassabb. És a hosszú úton a gyorsabb fény lehagyhatná a lassabbat, ennek a következménye az lenne, hogy csillag képe megkettőződne, a pályán távolodó csillag képét és a közeledőjét egyszerre látnánk, mert a fény a két esetből egyszerre érne ide. De más következményei is lennének, mint pl. a fénysugarak összetorlódnának, amely erőteljes felfénylést okozna meghatározott időnként. Viszont ilyet soha nem figyeltek meg, többféle kísérletet is terveztek ennek kimutatására, de mindegyiknek az volt az eredménye, hogy a fény terjedési sebessége mindig $c$ hozzánk képest, nincs forrás mozgásától függő gyorsulás vagy lassulás.
A dolgok összemennek
Adott a probléma. Ez a fény úgy tűnik minden nézőpontból nézve pontosan fénysebességgel megy, nem gyorsabban nem lassabban, és ez nagyon abszurd. Hogyan javíthatjuk meg a fizikát, hogy tartalmazza ezt a szokatlan tényt?
Először is ahogy fentebb levezettük, hogy a Michelson-kísérletnél kellene, hogy legyen időeltérés 2 irányban elindított fénysugarak között. De nincs. Ha mozog, ha nem mozog, a két fénysugár egyszerre fog visszaérni. Így viszont fentebbi egyenletben $\eqref{eq:paralleldir}$ igazítani kell valamit, hogy a két kapott idő megegyezzen. A $c$-hez nem nyúlhatunk, mert az nem függ a sebességtől, a $v$-hez sem. Csak az $L$-hez nyúlhatunk, a két időt úgy tehetjük egyenlővé, hogy az $L$-t elosztjuk $\gamma$-val. Azaz ha az apparátus mozog, akkor a menetirányban összemegy pont annyira, hogy a fény egyszerre érjen vissza. Bármennyire is hihetetlen ez, minden jel arra mutat, hogy ez így van.
Ha feltételezzük, hogy az apparátus a mozgás irányában összemegy, akkor a fénysugár mind a két irányban egyszerre ér vissza. A szimuláció a képre való kattintással indítható.
Ez az összemenés ad magyarázatot arra, hogy miért is hat erő a mágneses mezőben mozgó töltésre. Emlékezzünk vissza erre. A negatív töltés együtt mozog a vezetékben többi negatív töltéssel. A mi szemszögünkből a vezeték elektromosan semleges, de áram folyik benne, így mágneses mezőt kelt, ami a szintén mozgó töltésre erővel hat. A mozgó negatív töltés szemszögéből a vezetékben mozgó negatív töltések állnak. A vezetékben álló pozitív töltések pedig mozognak. A mi szemszögünkből a negatív töltések mozognak, tehát kicsit össze vannak nyomódva, ezért sűrűbben helyezkednek el. A mozgó negatív töltés szemszögéből viszont nem mozognak, így nincs összenyomódás, és ritkábban helyezkednek el, mint a mi szemszögünkből. A vezetékben álló pozitív töltések esetén a mi szemszögünkből állnak, nincs összenyomódás. A mozgó negatív töltések szempontjából a pozitív töltések mozognak és lesz összenyomódás, így ott nagyobb lesz a töltéssűrűség. Tehát a mozgó negatív töltés szempontjából ritkult a negatív töltések sűrűsége, de sűrűbb lett a pozitívaké. Ez azt jelenti, hogy a mozgó töltés szemszögéből hatni fog rá az elektromos erő. Így a paradoxon feloldható. A pontos levezetéshez egyelőre még nem mondtam el eleget.
A mi szemszögünkből a vezeték semleges, tehát a pozitív és negatív töltéshordozók sűrűsége egyenlő. Viszont az elektronok mozognak benne felfelé, ez áramot és mágneses mezőt okoz, amely a vezeték mellett szintén felfelé mozgó negatív töltést a vezeték felé téríti el. A negatív töltés szemszögéből viszont a pozitív töltések mozognak lefelé, a hosszrövidülés miatt a pozitív töltések sűrűbben lesznek. A negatív töltések viszont most már állnak, a negatív töltéshez képest, mert egy sebességgel mozognak. Így viszont a vezeték mellett lévő negatív töltés szemszögéből a vezetékben sűrűbben fognak elhelyezkedni a pozitív töltések, mint a negatívak, így a vezeték nettó pozitív töltésű lesz. Ez pedig elektromos vonzerőt jelent a negatív töltés számára.
Az idő lassabban telik
A kiinduló helyzetben a fény $2L / c$ idő alatt ért vissza. Aztán abban az esetben, amikor az apparátus mozog $2L / \sqrt{c^2 - v^2}$ idő alatt ért vissza. A kettő nem egyenlő. Ha ezt a kettőt elosztjuk egymással azt kapjuk, hogy az arány $c / \sqrt{c^2 - v^2}$ azaz $\gamma$ lesz.
Tehát a mozgó testek nem csak $\gamma$-szor rövidebbek lesznek, hanem $\gamma$-szor lassabban is telik bennük az idő. Kiderült, hogy nem csak a sebesség relatív, hanem a távolságok is, és az idő is.
Vannak részecskék, amelyek nagyon rövid ideig léteznek, mielőtt elbomolnak. Pl. ilyenek a müonok, amelyek a másodperc milliomod része alatt elbomolnak. Ezek akkor keletkeznek, amikor a világűrből érkező nagyon nagy energiájú részecskék a légkör atomjainak csapódnak. Ha a fény sebességével mennének, akkor is csak 300m-t tudnának megtenni. Azonban ezek a kozmikus részecskék mégis eljutnak a föld felszínéig. Ez azért van, mert számukra lelassul az idő, így van idejük eljutni a felszínig mielőtt elbomolnak. Az ő szemszögükből az egész világ nagy sebességgel mozog hátrafelé, így az, ami nekünk 30 km, nekik csak pár száz méternek felel meg a hossz rövidülése miatt.
A mi szemszögünkből a müonok gyorsak, ezért lelassul számukra az idő, így van idejük leérni a felszínig. A müon szemszögéből az egész világ nagy sebességgel megy vele szembe, így a világ a menetirányban összement a számukra, ezért az ő szemszögükből sokkal rövidebb a megteendő távolság a felszínig.
Ma már nagyon pontos atomórák vannak. Ha összeszinkronizálunk kettőt közülük, majd az egyiket elvisszük egy egy kis kocsikázásra már képesek kimutatni a relativisztikus időeltolódást. Azaz a megutaztatott órán néhány milliárdod másodperccel kevesebb idő telt el.
A műholdas helymeghatározó rendszerek is atomórákkal működnek. Ezek a műholdak annyit csinálnak, hogy sugározzák a nagyon pontos időt a Földre. Aztán a vevőegységek ebből kiszámolják, hogy hol vagyunk. Ahhoz, hogy a helymeghatározás pontos legyen, az kell, hogy ezek a rendszerek figyelembe vegyék a relativitás hatásait, különben pontatlan lesz a mérés.
Mindezt azért írtam, hogy nagyjából rávilágítsak, hogy bármennyire furcsa a hosszrövidülés és az időlassulás, ez tény. Így működik a természet, és minél mélyebbre megyünk, annál furcsább dolgokat tapasztalunk és mérünk. De erről majd később írok majd többet.
A dolgok nem feltétlenül történnek egyszerre
Vegyük a következő esetet: egy kamion konténerének a közepén felállítunk egy vakut. Majd miközben ez a kamion mozog a vakut elsütjük. A kamionból nézve a fény a vakuból az elülső és a hátulsó falat egyszerre éri el. Azonban kívülről nézve már nem egyszerre fogja elérni a két falat a fénysugár. Ami az egyik megfigyelő szemszögéből egyszerre történik, az a más sebességgel haladó megfigyelő szemszögéből már nem fog egyszerre történni. Persze ez csak akkor érvényes, hogyha a két esemény különböző helyen történik. Azon a tényen, hogy visszavert fénysugár egyszerre fog visszaérni, nem változtat az, hogy mozog a rendszer (mert az egy időben és egy helyen történik).
Állóhelyzetben a fénysugár egyszerre éri el a két tükröt és egyszerre ér vissza. Mozgó rendszer esetén különböző időpontokban érik el a fénysugarak tükröket, de egyszerre érnek vissza. Az animációk a képre való kattintással indíthatók.
Relativisztikus paradoxonok
A relativitás furcsaságaiból adónak bizonyos látszólag ellentmondásos helyzetek. Ebben a szekcióban ezeket nézzük majd meg kicsit alaposabban.
Az ikerparadoxon
Tegyük fel, hogy van egy ikerpár, az egyik csillagközi útra indul, és nagy sebességgel elkezd repkedni egy űrhajóval. Mivel nagy sebességgel repül, ezért lassabban telik számára az idő. Amikor visszaérkezik, akkor emiatt fiatalabb lesz, mint az a párja, aki itt maradt, és nem ment semerre. Viszont a mozgó iker szempontjából az egész világ mozog, még a Földön maradt társa is, és a Földön maradt párjának az órája jár lassabban. Akkor most kinek is kellene öregebbnek lennie?
A paradoxon megoldása az, hogy ez a szituáció nem teljesen szimmetrikus. Ugyanis a csillagközi út során, ha az ikerpárunk valóban haza szeretne menni, ahhoz vissza kell fordulnia. És ehhez sebességváltozásra lesz szüksége. És ez a gyorsulás egy másfajta időnyúlást, a gravitációs időnyújtást eredményezi. (Erről majd később bővebben.) És a hazaérkezéskor az idők különbsége elsősorban emiatt lesz.
Létraparadoxon
Van egy létránk, amely túl hosszú, hogy beleférjen a fészerbe. A megoldás: jó nagy sebességgel dobjuk be a fészerbe, a sebességtől rövidebb lesz, és akkor majd befér, és egy rövid időre rácsukjuk az elülső és a hátsó ajtót. Természetesen mivel nem szeretnénk felrobbantani a fészert a létrával, ezért gyorsan kinyitjuk az ajtót mielőtt nekicsapódna a falnak, hogy továbbrepüljön.
Viszont a létra szemszögéből meg a fészer megy össze, ő maga nem. Akkor most hogyan férhet be a fészerbe?
Itt az egyidejűség relativitása a trükk, a létra szemszögéből nézve ugyanis soha sem lesz egyszerre becsukva a két ajtó.
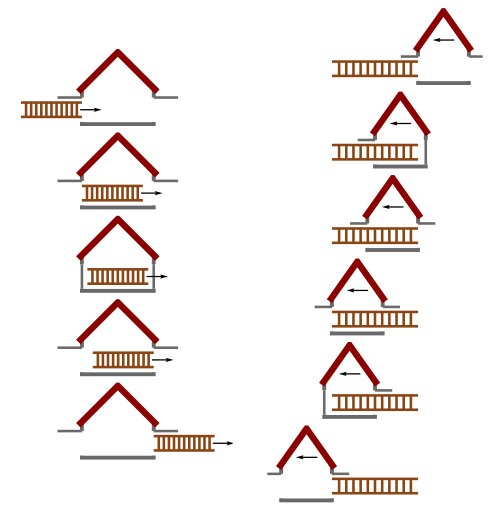
Az ún. létraparadoxon. A nagy sebességgel mozgó létra összemegy, így befér a garázsba, így egy rövid időre becsukhatjuk mind a két ajtót. A létra szemszögéből viszont a garázs megy össze, így még annyira sem férne be mint amúgy. Ebben a paradoxon úgy oldható fel, hogy az ajtók nem egy időben fognak az ő szemszögéből záródni. (forrás, forrás)
Kötelékrepülés paradoxon
Tegyük fel, hogy van két azonos fajta űrhajónk. Amelyek egymástól 1 km-re vannak és egyszerre elkezdenek gyorsítani. Mivel mindenben azonosak, azért teljesen azonos módon fognak gyorsulni. Így a mi szemszögünkből tartják a távolságot. Ahogy egyre gyorsabbak lesznek, úgy viszont összemennek az űrhajók. Viszont hogyhogy nem az egész kötelék megy össze?
Az igazság az, hogyha a két űrhajó össze lenne kötve egy kötéllel, akkor a teljes kötelék összemenne, és ebből adódóan nem tudnának egyszerre pontosan azonos gyorsulással gyorsulni. Ebben az állapotban a két űrhajó szemszögéből a távolságuk azonos marad. Ha viszont nincsenek összekötve, akkor hiába az azonos gyorsulás, eltávolodnak egymástól. Később majd ha már ismerjük a téridőt, jobban le lehet ezt majd írni.
Relativisztikus lendület
Mivel a mozgó rendszerben lelassul az idő, ezért minden fizikai folyamat is lassulni látszik. Még maga a sebesség is. Ha $\gamma = 2$, akkor az azt jelenti, hogy test fele olyan gyorsan megy, mint ahogy menne, hogyha nem lenne ez a relativisztikus időnyúlás. A $\gamma$ akkor 2, amikor a test a fény sebességének kb. a 87%-ával megy. Szóval elég nagy a sebesség. Ha nem lenne relativitás, akkor a test a fénysebesség 173%-ával menne. Viszont attól, hogy a relativitás miatt lassabban megy, a lendülete ugyanúgy annyi, mintha valóban a fénysebesség 173%-ával menne. Tehát a lendület nem $m v$, hanem $m \gamma v$ ($m$: tömeg, $v$: sebesség, $\gamma$: korrekciós tényező).
Ennek természetesen az a következménye, hogy emiatt a lassulás miatt az erők is látszólag kisebb gyorsulást képesek csak létrehozni rajta, mintha megnőtt volna a tömege. Viszont ezzel óvatosan, mivel ez bizonyos tömeg mozgásra merőlegesen $\gamma$-szor a mozgás irányában pedig $\gamma^3$-szorosan növekedett meg. Emiatt egyáltalán nem helyes azt mondani a nagy sebességtől megnő a tömeg, mivel ezzel sok problémát okozhatunk maguknak és sok dolgot félreérthetünk.
A fénysebesség az elérhető legnagyobb sebesség
Szokták mondani, hogy fénynél gyorsabban nem lehet menni, most levezetem, hogy miért is. Induljunk ki a relativisztikus lendület képletéből, és alakítgassuk addig, amíg ki nem tudjuk belőle nyerni a $v$-t. Íme az átalakítgatás:
$$ p = \gamma m v \\ p = {m v c \over \sqrt{c^2 - v^2}} \\ p^2 = {m^2 v^2 c^2 \over c^2 - v^2} \\ p^2 \left( c^2 - v^2 \right) = m^2 v^2 c^2 \\ p^2 c^2 - p^2 v^2 = m^2 v^2 c^2 \\ p^2 c^2 = m^2 v^2 c^2 + p^2 v^2 \\ p^2 c^2 = v^2 \left ( m^2 c^2 + p^2 \right ) \\ v^2 = {p^2 c^2 \over m^2 c^2 + p^2} \\ $$
Na most mi van akkor, hogyha a testet gyorsítjuk, gyorsítjuk és gyorsítjuk, és a lendülete egyre nagyobb és nagyobb lesz? Látható, hogyha a $p$ hatalmas lesz, akkor a mellette lévő $m^2 c^2$ tag egyre elhanyagolhatóbbá válik hozzá képest. Így a tört lényegében a $p^2 c^2 \over p^2$ felé tart, amely pedig egyszerűsítés után $c^2$ lesz. Azaz $v^2$ tart $c^2$ felé, vagyis $v$ tart $c$ felé. A sebesség tart a fénysebesség felé, de soha sem éri el azt. Arról pedig szó sem lehet, hogy meghaladja.
További érdekesség, hogy a fénynek nincs tömege, viszont mégis szállít lendületet és energiát is. Ebből adódóan a fenti képletben az $m$-es tag, amely előbb fokozatosan egyre elhanyagolhatóbbá vált, alapból nincs is ott. Így a fény, ha véges lendülettel is, legyen az bármilyen pici, alapból $c$-vel, azaz fénysebességgel megy. Más sebességgel nem is mehet!
Az energia tömege
Ebben a szekcióban nem teszünk más, mint azt, hogy levezetjük az egyik leghíresebb képletet. Amit talán mindenki látott már, de sokan nem értik, hogy honnét is jön.
Legyen két azonos $m$ tömegű testünk. Menjenek $v$ sebességgel. Az egyik jobbra menjen, a másik balra menjen. Majd ütközzenek ezek össze teljesen rugalmatlanul. Azaz a mozgási energia egy része vagy egésze deformálásra és hőfejlődésre fordul majd.
A $v$ sebességhez tartozó korrekciós tényező legyen $\gamma$. Tehát az egyik test lendülete $m \gamma v$. A másiké pedig $- m \gamma v$, mert a másik irányban halad. A rugalmatlan ütközés után a két test úgy ragad össze, mint 2 gyurmatömb. A lendület pedig megmarad. És mivel 2 azonos nagyságú de ellenkező előjelű lendületről van szó, az összeg 0. Tehát az ütközés után lesz egy álló anyagtömbünk.
Most nézzük ugyanezt egy olyan szemszögből, amikor egy pici $\epsilon$-nyi sebességgel mozgunk lefelé. Ekkor a testek a vízszintes sebességek mellett még $\epsilon$ sebességgel mozognak felfelé, és az ütközés után a nagy anyagtömb is $\epsilon$ sebességgel mozog majd. Tehát ilyenkor a test sebességét vektorként kell kezelni és az egyiké $\v v = (v_x, \epsilon)$ lesz. A másiké $\v u = (-v_x, \epsilon)$ lesz. A $v_x$ a vízszintes sebesség most. Mivel ezen vektorok tagjai azonos nagyságúak (csak az előjelekben van különbség), ezért a két sebesség nagysága azonos, és a hozzá tartozó $\gamma$ korrekciós tényező is ugyanaz lesz. Így az egyik tesz lendülete $m \gamma \v v$, a másiké pedig $m \gamma \v u$ lesz. Ütközés után kialakuló tömeg lendülete ezen kettő összege lesz azaz: $m \gamma \v v + m \gamma \v u = m \gamma (\v v + \v u)$. A két sebességvektor összege pedig: $(-v_x, \epsilon) + (v_x, \epsilon) = (0, 2 \epsilon)$. Az $m \gamma$-val való szorzást elvégezzük: $(0, 2 m \gamma \epsilon)$. Tehát lesz végeredményben kapott testnek egy $2 m \gamma \epsilon$ lendülete felfelé, ebből a nézőpontból. Ahogy mondtuk a sebesség ebben a nézőpontban $\epsilon$ lesz felfelé. Mivel az $\epsilon$ pici, ezért most a relativisztikus hatások elhanyagolhatóak, és a lendület kezelhető tömeg és sebesség szorzataként. Ebből viszont az következik, hogy a test tömege $2 m \gamma$. Azaz több, mint az őt alkotó két test tömege (mert amúgy csak $2m$-nek kéne lennie).
De mennyi a $\gamma$? Ez ugye az eredeti sebességhez tartozó tényező. Annak tagjai $(v_x, \epsilon)$ voltak. Ennek a vektornak a négyzete a tagjai négyzetének az összege, azaz: $v_x^2 + \epsilon^2$ lesz. Behelyettesítve a $\gamma$ képletébe:
$$ \gamma = {c \over \sqrt{c^2 - v_x^2 - \epsilon^2}} $$
De mivel az $\epsilon$ pici a fénysebességhez és a $v$-hez képest, ezért nagyon nem tud beleszólni az értékbe, így elhanyagolható a képletből. És használhatjuk simán a $v$-hez tartozó $\gamma$-t:
$$ \gamma = {c \over \sqrt{c^2 - v_x^2}} $$
Minél nagyobb sebességgel csattan össze a két test, annál nagyobb lesz a $\gamma$, és annál nagyobb lesz kapott anyagkupac tömege. Honnét jön ez a tömegnövekedés? Talán köze lehet az ütközés során a testben deformálásra és hőfejlesztésre fordult energiával. Magából a $\gamma$-ból nem sok olvasható ki úgy önmagában, viszont, hogyha képezzük a $\gamma$ hatványsorát (amiről egy másik posztban itt írtam), akkor ezt kapjuk:
$$ \gamma = 1 + {v^2 \over 2 c^2} + {3 v^4 \over 8 c^4} + {5 v^6 \over 16 c^6} + ... $$
Szorzunk a tömeggel:
$$ m \gamma = m + {m v^2 \over 2 c^2} + {3 m v^4 \over 8 c^4} + {5 m v^6 \over 16 c^6} + ... $$
Illetve még $c^2$-tel is, és akkor látunk majd egy ismerős tagot a képletben:
$$ m \gamma c^2 = m c^2 + {m v^2 \over 2 } + {3 m v^4 \over 8 c^2} + {5 m v^6 \over 16 c^4} + ... $$
Ez a tag az ${m v^2 / 2}$ azaz a mozgási energia képlete. Ha a $v$ kicsi, tehát a sebesség mindennapi életben tapasztalt sebességek, akkor a $c^2$-tel és a $c^4$-nel osztott tagok elhagyhatóak, mert olyan picik lesznek. Ne feledjük, hogy a $c^2$ = 90 000 000 000 000 000 m${}^2$/s${}^2$. A negyedik hatványban meg még kétszer ennyi nulla van. Ha ezeket a magasabb rendű tagokat elhagyjuk, akkor marad az, hogy:
$$ m \gamma c^2 = m c^2 + {m v^2 \over 2 } + ... $$
Mozgási energia pedig némi algebrai rendezés után kifejezhető:
$$ m \gamma c^2 = m c^2 + {m v^2 \over 2 } + ... \\ m \gamma c^2 - m c^2 = + {m v^2 \over 2 } + ... \\ m (\gamma - 1) c^2 = {m v^2 \over 2 } + ... \\ $$
Az $m (\gamma - 1)$ pedig nem más, mint az extra tömeg, ami bejött. Ennek a $c^2$-szerese pedig a mozgási energia. Ez épült be a tömegbe.
És innét jön a híres képlet, mely szerint:
$$ E = m c^2 $$
Azaz a tömeg és az energia ugyanaz. Csak más skálán mérjük őket. A mindennapi életben túl kicsi energiák vannak ahhoz, hogy mérhető tömegnövekedést okozzanak, de a kémiában és az atomfizikában megszokott dolog, hogy egy összetett rendszer kisebb tömegű, mint az őt alkotó részek tömege. Pl. a hélium atom könnyebb, mint az azt alkotó 2 proton, 2 neutron és 2 elektron külön-külön. Mert a különbözet felszabadul, amikor ezek az alkotóelemek összeragadnak egy csillagban vagy egy hidrogénbombában, ettől süt a Nap tulajdonképpen.
A következő egy vagy két részben egy kicsit mélyebben is belemegyünk majd ebbe, és szó lesz a téridőről. Addig is érdemes elgondolkodni a leírtakon és mélyebben magunkévá tenni, mert a következő részekben erősen ráépítünk majd ezekre.