7. Mozgás
Fizikának és még nagyon sok tudománynak fontos része a változások tanulmányozása. Változás minden, ami... változik. Ebben a részben azzal fogunk foglalkozni, hogy hogyha lehet a változást matematikailag leírni, hogyan lehet számolni vele.
Mozgás leírása
Először is mi is a mozgás. Ez tulajdonképpen egy adott tárgy helyének a megváltozása, miközben telik az idő.
Amikor mozgásról beszélünk, akkor általában olyan dolgok mozgásáról beszélünk, amelyek pontszerűnek tekinthetők az általuk bejárt úthoz képest. Pl. egy autó lényegében pontszerű, hogyha az általa megtett 100 km úthoz viszonyítjuk. Ezt csak azért írom le most, hogy ne kelljen kiakadni azon, hogy most a megtett utat az autó elejéhez vagy hátuljához képest mérjük-e.
Hogyan írhatjuk le a mozgást? Pl. táblázatos alakban. Rögzíthetjük az eltelt időt és egy autó által megtett távot:
| Idő | Táv |
|---|---|
| 1 perc | 500 m |
| 2 perc | 1300 m |
| 3 perc | 1300 m |
| 4 perc | 1900 m |
| 5 perc | 2900 m |
| 6 perc | 3500 m |
| 7 perc | 4100 m |
| 8 perc | 5100 m |
| 9 perc | 7100 m |
Vagy az előzőt megadhatjuk grafikonnal is:
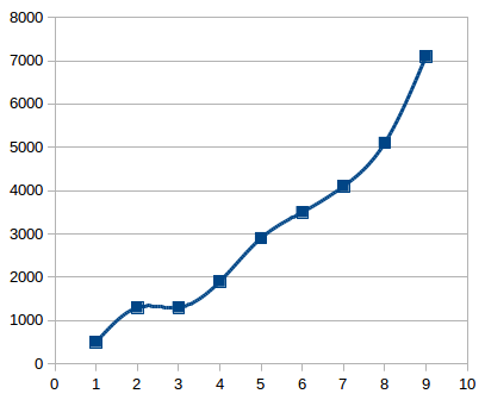
Megtett út az idő függvényében.
Már ebből is láthatjuk, hogy nagyjából milyen mozgást végzett az autó. Ebből a táblázatból nem tudjuk pontosan megmondani, hogy az autó milyen gyorsan ment az egyes időpontokban, pl. 1 perc 34 másodperckor, de a trendek jól láthatók. Látható pl. hogy 2 és 3 perc között nem ment semerre, talán mert piros lámpát kapott. Aztán lehet látni, hogy innentől kezdve különféle sebességekkel megy. A végén már egész gyorsan megy, nyilván azért, mert felhajtott mondjuk egy autópályára.
Vannak másfajta mozgások is, amelyek pontosan leírhatóak. Ilyen pl. egy leejtett szabadon eső labda. Nézzük meg az ahhoz tartozó táblázatot:
| Idő | Táv |
|---|---|
| 0 mp | 0 m |
| 1 mp | 5 m |
| 2 mp | 20 m |
| 3 mp | 45 m |
| 4 mp | 80 m |
| 5 mp | 125 m |
| 6 mp | 180 m |
A labda leesése egyébként egzakt. Nagyjából képlettel kifejezhető: $s = 5t^2$. Ahol $s$ az elmozdulás, $t$ az eltelt idő.
Ha elvonatkoztatunk a konkrét képlettől, akkor mondhatjuk azt, hogy az elmozdulás az idő valamilyen függvénye. Matematikailag: $s = f(t)$. Az $f(t)$ egy tetszőleges algebrai kifejezés, amely tartalmazza a $t$ változót (mint pl. az $5t^2$). Tehát a mozgás tulajdonképpen egy összefüggés a tér az idő között.
Ilyenkor felmerülhet a kérdés, hogy tulajdonképpen mi is a tér, és mi is az idő. A 20. század elején a relativitás elmélettel eléggé meg lett bolygatva ez a kérdés. Most egyelőre még nem tartunk ott, hogy a relativitást tárgyaljuk, majd talán később. Most egyelőre elég az, hogyha a tér és a távolságok azt jelentik, amit egy méterrúddal vagy vonalzóval megmérhetünk. Míg az idő az, amit az órákkal mérhetünk. Ezekről a témákról a 4. részben írtam már.
Sebesség
Talán a sebességet nem kell elmagyarázni. Ez az a dolog, amit az autók sebességmérője mutat, és egy csomó helyen ki van táblázva, hogy mennyivel lehet menni. Ha pedig túl léped a megengedett sebességet, akkor jön a csekk.
Azért ez nem volt mindig ilyen magától értetődő. A görögök sok dolgot feltaláltak, de a sebesség fogalma már kicsit meghaladta a képességeiket. Zénó számos sebességgel kapcsolatos paradoxont mondott ki. Az egyik talán legismertebb az Akhilleusz és a teknős esete.
Ez a dolog a következőképpen fogalmazható meg (a történet nem pontosan úgy van, mint az eredeti): A teknős és Akhilleusz versenyeznek. Akhilleusz 10-szer gyorsabb, mint a teknős. Ezért, hogy valamelyest kiegyenlített legyen a dolog Akhilleusz előre engedi a teknőst 100 méterrel. Ki nyeri a versenyt? Amint a verseny elindul Akhilleusz megtesz 100 métert, addigra a teknős megtesz 10 métert. Ezután Akhilleusz fut 10 métert, de a teknős eközben megtesz 1 métert. Majd Akhilleusz fut 1 métert, de eközben a teknős megint előre ment 0,1 métert. És ez megy a végtelenségig, úgy tűnik, hogy Akhilleusz soha sem fogja utolérni a teknőst.
Gondolom mindenki érzi, hogyha valami gyorsabb, mint én, akkor az előbb vagy utóbb utol fog érni. Attól, hogy végtelen sok lépésből áll a mozgás leírása még nem jelenti azt, hogy végtelen sokáig fog tartani. Akhilleusz 111 és még egy kilenced méter után utol fogja érni a teknőst, véges időn belül.
De nézzük meg egy másik esetet. 1A következő történetet a Feynmann-lectures Vol 1 8. előadásából vettem. Némi módosítással. Tegyük fel, hogy megállít a rendőr egy autóst, mert 180 km/h-val ment a megengedett 130 helyett. A rendőr kérdőre vonja, hogy: „Van fogalma arról, hogy olyan gyorsan ment, hogy 180 km-t tesz meg óránként?” A válasz pedig kérdésre az lehet, hogy: „Az nem lehet, hiszen még csak 10 perce vagyok úton, kizárt, hogy 180 km-t tettem meg ez idő alatt!” Most tegyük fel, hogy a rendőr és az autós is fizikus, és megpróbálja megértetni az autóssal, hogy még is mi a fene az a 180 km/h. Tehát a rendőr válasza: „Tehát, ha ön továbbra is úgy menne, mint ahogy most ment, akkor 1 óra múlva 180 km-t tenne meg.” Az autós erre azt mondaná: „Levettem a lábam a gázpedálról, lelassultam és megálltam. Ebben az állapotban tuti, hogy nem tennék meg 180 km-t egy óra alatt.” Tulajdonképpen mit is jelent az, hogy „úgy mozogna tovább, ahogy abban a pillanatban mozgott”? Pl. ha egy golyó esését nézzük, az egyre gyorsabb és gyorsabb és gyorsabb lesz. Tehát mi nem egészen erre gondolunk, hanem arra, hogy úgy megyünk tovább, hogy a sebességünk nem változik. Tehát a rendőr következő próbálkozása: „Jó, akkor tegyük fel, hogy nem vette le a lábát a gázpedálról, nem gyorsít, nem lassít. Na ha így menne tovább 1 óráig, akkor 180 km-t tenne meg!” Erre az autós válasza: „Ha nem lassulnék le, 1 óráig, akkor beleszaladnék abba a házba az út végén!” Hát nincs egyszerű dolgunk...
A tudományban mindennek az alapja a mérés és a kísérletezés, így a következő próbálkozásunk az lehet, hogy: „Figyeljen! A sebességmérője 180 km/h-t mutatott!” Erre az autós válasza: „A sebességmérőm elromlott az nem mutatott semmit. Tehát nem mehetettem annyival...”. Attól, hogy a sebességmérő nem működik az nem jelenti azt, hogy az autó áll. Nyilvánvalóan ahhoz, hogy egyáltalán azt mondhassuk, hogy sebességmérő nem működik először is kell, hogy legyen valami, amit sebességmérő mér. A következő próbálkozás „Na, akkor tegyük fel, hogy nem vette le a lábát a gázpedálról, nem gyorsít, nem lassít. Na ha így menne tovább csak 1 másodpercet, akkor 50 m-t tenne meg!” Erre az autós válasza: „De hát arra nincs szabály, hogy nem tehetek meg 50 métert másodpercenként! ” Erre rögtön mondhatjuk azt, hogy „A kettő teljesen ugyanaz!”
$$ 180 \frac{\mathrm{km}}{\mathrm{h}} = 180 \frac{1000 \mathrm{m}}{3600 \mathrm{s}} = \frac{180000 \mathrm{m}}{3600 \mathrm{s}} = 50 \frac{\mathrm{m}}{\mathrm{s}} $$
Ekkor már valamelyest jó úton vagyunk, hogy hogyan definiáljuk a sebességet precízen. Tehát venni kell egy távolságot, és meg kell mérni az időt, amennyi idő alatt átmegy rajta, és így megkapjuk az átlagsebességet, amivel a jármű ez alatt az időtartam alatt ment. Egy autó esetén az 1 másodperc alatt megtett táv elég jól megadja a pillanatnyi sebességet, mert egy autó sebessége nem változik túl gyors ütemben. Azonban egy szabadon eső test esetén ez a megoldás már pontatlan. Minél kisebb időtartam alatt megtett távolságot veszünk annál jobb. Egy 180 km/h-val haladó autó egy ezredmásodperc alatt 5 centimétert tesz meg. Ez nagyon rövid időtartam, ennyi idő alatt nem tud számottevően változni a sebesség. De ez még mindig nem precíz definíciója a sebességnek.
Ha precízen akarjuk definiálni a sebességet, akkor egy olyan technikához kell folyamodnunk, amelyet még a görögök sem ismertek. Ha a sebességet le akarjuk írni, akkor minél kisebb időtartamot nézünk annál jobb. Végtelenül pici időtartamot kell venni. Ez alatt a végtelenül pici időtartam alatt az elmozdulás is végtelenül pici. De ha a kettőt elosztjuk egymással, akkor megkapjuk a pontos sebességet.
A végtelenül pici dolgok matematikáját a 17. században találták fel az akkor élő matematikusok, Newton, Leibniz és még sokan mások. Ez a differenciál kalkulus, amelyet az elsők között alkalmazták arra, hogy pontosan és precízen tudják definiálni a sebességet.
Korábban felírtuk a képletet, hogy egy szabadon eső golyó valamilyen $t$ idő alatt $5t^2$ utat tesz meg. Tehát 1 másodperc alatt 5 métert; 2 alatt, 20-at; stb. Na most akkor mennyi a sebesség egy valamilyen adott időpontban?
Ahogy az előbb írtuk a trükk az, hogy megnézzük, hogy mennyi utat tesz meg egy nagyon pici időtartam alatt. Majd ezt az utat elosztjuk a nagyon pici időtartammal.
Tegyük fel, hogy a 3. másodpercben vagyunk. A képlet szerint a szabadon eső test 45 métert esett eddig. Hol leszünk egy ezred másodperc múlva, tehát 3,001 másodpercnél? A képlet szerint 45,030005 méternél. Tehát 1 ezred másodperc alatt esett a golyó 3 centit. Azaz pontosan 45,030005 - 45 = 0,030005 métert. Ezt elosztva a 0,001 másodperccel, ami eltelt azt kapjuk, hogy 30,005m/s.
Ez egyébként majdnem ott van, ahol a helyes válasz, de még mindig nem precíz. Legyen $\epsilon$ egy nagyon piciny időtartam. Ekkor a 3. másodperc után egy $\epsilon$-nyi idő elteltével a megtett táv: $5(3+\epsilon)^2 = 5(9 + 6\epsilon + \epsilon^2) = 45 + 30\epsilon + \epsilon^2$. Tehát a piciny időtartam alatt megtett út $30\epsilon + \epsilon^2$. Ezt elosztjuk a piciny $\epsilon$ időtartammal azt kapjuk, hogy $30 + \epsilon$. Na most az $\epsilon$ pici, rendkívül pici, kisebb, mint bármilyen pozitív szám, de nagyobb, mint 0. Gyakorlatilag nulla, de mégsem, mert 0-val nem lehet osztani, $\epsilon$-nal meg lehet. Így gyakorlatilag elhagyható az egyenletből, és így marad a 30. Azaz 30m/s. Ami a helyes válasz a kérdésre.
Vagy ha általánosabban akarjuk, akkor elvégezhetjük ezt az általános képlettel is. Tetszőleges $t$ időpontban az esés $5t^2$. Egy picivel arrébb $t+\epsilon$ időpontban: $5(t + \epsilon)^2 = 5(t^2 + 2t\epsilon + \epsilon^2) = 5t^2 + 10t\epsilon + 5\epsilon^2$. Az $\epsilon$ alatt megtett út $10t\epsilon + 5\epsilon^2$. $\epsilon$-nal elosztva pedig $10t + 5\epsilon$-t kapunk. Mivel az $\epsilon$ pici ezért marad a $10t$, ami a képlet a szabadon eséskor a sebességre.
Sebesség mint derivált
A fizikában egy mennyiség valamilyen változását úgy szokták jelölni, hogy elé írnak egy $\Delta$-t. Tehát az előző esetben az idő változása $\Delta t$. Ez a $\Delta$ nem szorzás, hanem része a tagnak. Egyszer vagyunk $t$ időpontban, aztán kicsivel később $t + \Delta t$ időpontban vagyunk. Szintén az elmozdulás $s$, míg egy kicsi elmozdulás után $s + \Delta s$ helyen vagyunk. Tehát, ha $s = f(t)$, akkor hasonlóképpen: $s + \Delta s = f(t + \Delta t)$. Ez a deltázás azért jó, mert ezen lehet látni, hogy melyik mennyiség változásáról van szó. Míg az előbb külön meg kellett magyarázni, hogy az $\epsilon$ az idő pici változása.
Ha $\Delta t$ nagyon pici, akkor így megkapjuk a sebesség formuláját. Ez ugyanaz, mint előbb csak pepitában:
$$ v = \lim_{\Delta t \rightarrow 0} \frac{\Delta s}{\Delta t} $$
Azaz $\newcommand{\d}{\mathrm{d}}$ a rövid idő alatt megtett utat elosztjuk azzal a rövid idővel. Ezt a deltás jelölést akkor használjuk, hogyha a mennyiség nem nullához közeli. Hogyha kifejezetten nullához közeli mennyiségről van szó, akkor $\d$ előtagot szokás használni. Így eljutunk a szokásos jelöléshez:
$$ v = \frac{\d s}{\d t} $$
Mivel ez a $\d$ előtagú mennyiség eleve nullához közeli. Nincs szükség a határértékre. Két pici mennyiség hányadosa már lehet nagy. Ez a differenciálhányados. Ez a szokásos formája a deriválásnak. A fentit úgy szokás olvasni, hogy $s$-nek a $t$ szerinti deriváltja. Vagy az elmozdulás idő szerinti deriváltja.
Ez deriválás olyan fontos dolog a fizikában, hogy érdemes mélyebben beleásnunk magunkat, hogy megértsük a lényegét. Illetve arról is, hogy hogyan kell azt használni, hogy elkerüljük a későbbi félreértéseket.
Deriválás lényege
Van két mennyiségünk, változónk, jelöljük az $x$-szel és $y$-nal. Ezek között pedig van valamilyen összefüggés: $y = f(x)$. Tehát $y$ egyenlő valamilyen, tetszőleges, $x$-től függő kifejezéssel, amit $f$-fel jelöltünk.
Ha az egyik változó megváltozik, a képletben más szám lesz így a másik változó is megváltozik. Jelöljük $\Delta x$-szel az $x$ változását, $\Delta y$-nal az $y$ változását, így a változtatás után ez az egyenlet: $y + \Delta y = f(x + \Delta x)$
Kivonjuk egymásból a 2 egyenletet, és megkapjuk $y$ változását az $x$ és $\Delta x$-től függően: $\Delta y = f(x + \Delta x) - f(x)$. Elosztva ezt $\Delta x$-szel megkapjuk a két változás egymáshoz képesti viszonyát:
$$ \frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) - f(x)}{\Delta x} $$
És erről szól a deriválás, két egymástól függő mennyiség változásának viszonyát írja le. Mint pl. a hely és az idő változásának a viszonya a sebesség. Ahhoz, hogy az eredmény pontos legyen, a változásnak picinek kell lennie. Így a deltás tagoknak nullához kell tartani:
$$ \frac{\d y}{\d x} = \lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} $$
És ez az a képlet, amit úgy gyorsan fel szoktak hányni analízis órán, és gyakran nem magyarázzák meg, hogy honnét is jön...
Célszerű ezen két pici változás hányadosára, a $\frac{\d y}{\d x}$-re, úgy tekinteni, mint az $y$ mennyiség változásának sebességére. Ha a nevező az idő pici változása, a $\d t$, áll, akkor ez a hétköznapi értelemben vett sebesség. Ha valami gyorsabban történik, ott ez a hányados nagy; ha lassabb, kisebb; ha áll, nulla; ha negatív akkor meg fordított irányban történik.
Azonban a nevezőben nem csak az idő pici változása állhat. Nézzünk egy másik példát: a domborzat meredeksége. Hogy írnánk le matematikailag, hogy milyen meredek egy domb? Állunk egy pontban, ott valamennyi a tengerszint feletti magasság. Egy picit előre megyünk, és megnézzük, hogy a tengerszint feletti magasság mennyit változott. Nyilván ez is egy picit fog csak változni. A kettőt elosztjuk és megkapjuk a domb meredekségét abban az irányban. Vagy technikailag fogalmazva a domb szintjének az emelkedésének a sebessége a térben. Ha ez a hányados nagy, akkor a domb meredeken emelkedik; ha kisebb, akkor kevésbé meredeken; ha nulla, akkor a táj vízszintes; ha negatív, akkor pedig lejt.
Későbbiekben nagyon sokszor fog kelleni az analízis, így már jobb most megnézni pár gyakorlati dolgot, hogy hogyan lehet használni ezt a matematikai eszközt. Ugye azt mondtuk, hogyha van egy mennyiségünk $x$, és ha ezt a mennyiséget kicsit megváltoztatjuk, a változást úgy jelöljük, hogy $\d x$. Ezzel a pici változással az a pici probléma van, hogy olyan szám nincs, hogy „pici”. Csak akkor lehet kicsi dolgokkal valami értelmeset csinálni, hogyha más pici dolgokkal hasonlítjuk össze. Tegyük fel, hogy van két mennyiségünk $x$ és $y$, mindegy micsoda, valami. És van egy feltételünk vele kapcsolatban, egyszerűség kedvéért legyen: $x = y$. Ha megváltoztatjuk $x$-et, akkor $y$-nak is pontosan ugyanúgy kell változnia, hogy az egyenlőség fennálljon. Tehát $\d x = \d y$, függetlenül attól, hogy ez a két mennyiség mennyire pici. Vagy akár átrendezhetjük ezt ismerősebb alakba és mondhatjuk azt, hogy: $\frac{\d y}{\d x} = 1$. Ez nem feltétlenül szükséges. Sokszor intuitívabb ezekben a pici dolgokban gondolkodni, mint mindenképp megkövetelni, hogy két pici dolog hányadosként szerepeljen az egyenletben minden pillanatban. A következőkben megvizsgáljuk néhány kifejezés pici változását, és meghatározunk néhány szabályt, amelyet a későbbiekben alkalmazni is fogunk.
Összeg és különbség differenciája
Van két mennyiségünk, legyen az $x$ és $y$. legyen az összegük $z$. Tehát $z = x + y$. Ha az $x$-et megváltoztatom $\Delta x$-szel, az $y$-t megváltoztatom $\Delta y$-nal, akkor a $z$-nek is meg kell változnia $\Delta z$-vel. Tehát a változás után az egyenlet: $z + \Delta z = x + \Delta x + y + \Delta y$. Ha ezt a két egyenletet kivonjuk egymásból, akkor megkapjuk, hogy $\Delta z = \Delta x + \Delta y$. Ez nem változik számottevően, hogyha feltételezzük, hogy ezek a változások nagyon picik, tehát: $\d z = \d (x+y) = \d x + \d y$. Tehát ha két mennyiség változik, akkor az összegük változása a változások összege. Nyilván különbséggel ugyanez van.
Szorzat differenciája
Ismét van két mennyiségük csak most a szorzatukat vesszük: $z = xy$. Ha megváltoztatjuk $x$-et és $y$-t, akkor a $z$ is változik, és az egyenlet ez lesz: $z + \Delta z = (x + \Delta x)(y + \Delta y)$. A két egyenlet különbsége: $\Delta z = (x + \Delta x)(y + \Delta y) - xy$. Ha a zárójelet felbontjuk és összevonjuk a tagokat ez marad: $\Delta z = x \Delta y + y \Delta x + \Delta x \Delta y$. Ha pici a változás, akkor van egy kis trükk. Piciből is sokféle van. Van pici és van a nagyon pici, (meg az ennél is picibb). Ha két picit összeszorzunk, akkor az még kisebb lesz. A 0,00001 * 0,00001 = 0,0000000001. Ha valami pici, akkor az nem befolyásolja nagyobb számok nagyságrendjét. Tehát a fenti példában a $x \Delta y$ és a $y \Delta x$ pici. A $\Delta x \Delta y$ pedig nagyon pici, mert két pici dolog szorzata. Így csak a sima picik maradnak meg. Így a végeredmény: $\d z = \d (xy) = x \d y + y \d x$. Persze ez az elhagyogatás csak akkor működik, hogyha azzal nem hozunk létre nullát sehol sem az egyenletben.
Hányados differenciája
Ismét van két mennyiségük csak most a hányadosát vesszük: $z = x/y$. Ha megváltoztatjuk $x$-et és $y$-t, akkor a $z$ is változik, és az egyenlet ez lesz: $z + \Delta z = \frac{x + \Delta x}{y + \Delta y}$. A két egyenlet különbsége: $\Delta z = \frac{x + \Delta x}{y + \Delta y} - \frac{x}{y}$. Közös nevezőre hozás után: $\Delta z = \frac{xy + y \Delta x - xy - x \Delta y}{y^2 + y \Delta y}$. Az $xy$ tag kiesik: $\Delta z = \frac{y \Delta x - x \Delta y}{y^2 + y \Delta y}$. Ha a változás kicsi, akkor a nevezőben az $y \Delta y$ tag elhanyagolhatóan pici lesz lesz $y^2$-hez képest, így kiesik. Tehát $\d z = \d (x/y) = \frac{y \d x - x \d y}{y^2}$.
Hatvány differenciája
Ismét van két mennyiségünk, az egyik valamilyen $n$. hatványa a másiknak: $y = x^n$. Ha megváltoztatjuk $x$-et $y$-nak is muszáj lesz változnia: $y + \Delta y = (x + \Delta x)^n$. Ha a zárójelet felbontjuk, akkor kapunk valami ilyesmit: $y + \Delta y = x^n + n x^{n-1} \Delta x + R$. A két egyenlet különbsége: $\Delta y = n x^{n-1} \Delta x + R$. Ahol az $R$ tartalmazza a többi tagot, azokban a $\Delta x$ nagyobb hatvánnyal (legalább négyzeten) szerepel. Ha $\Delta x$ pici, akkor az $R$ tag kiesik, mert abban nagyon pici és nagyon-nagyon pici tagok vannak, míg az összegben a legnagyobb nagyságrendű tag szimplán pici. Tehát $\d y = n x^{n-1} \d x$. Ha elosztunk a $\d x$-szel, akkor megkapjuk a szokványos képletet: $\frac{\d y}{\d x} = n x^{n-1}$.
Konstans differenciája
A konstansok olyan dolgok, amelyeknek egy adott konkrét értékük van. Pl. a 3-as szám az mindig 3 lesz. Soha nem változhat meg. A 3 az mindig 3. Éppen ezért a konstansoknak a differenciája 0. $\d 3 = 0$. Ez csak azért érdekes, mert a korábban említett azonosságok alapján előfordulhat ilyen. Pl. $\d (a+b) = \d a + \d b$. Ekkor ha venni akarjuk, pl. az $x + 2$ differenciáját: $\d(x + 2) = \d x + \d 2 = \d x$. Mert, ugye, a konstans differenciája 0.
Konstanssal alkotott szorzat differenciája
Van egy mennyiségünk, amit megszorzunk egy fix számmal. Hogyan hat ez a szorzás a differenciára? Tehát legyen a mennyiség $x$. Szorozzuk be mondjuk 3-mal, és legyen ez a másik mennyiség $y$: $y = 3x$. Ha megváltoztatjuk $x$-et $y$-nak is muszáj lesz változnia: $y + \Delta y = 3(x + \d x) = 3x + 3\d x$. A két egyenlet különbsége: $\d y = 3 \d x$. Tehát, ha a mennyiséget szorozzuk egy számmal, akkor az a differenciáját is szorozza.
Akármi differenciája
Tegyük fel, hogy egy tetszőleges mennyiségünk tetszőleges képlettel, ami függ sokféle változótól, amelyeket jelöljük rendre, $a$, $b$, $c$, stb.-vel: $y = f(a, b, c, ...)$. Ha bármelyiket megváltoztatjuk, $y$ is változhat így: $y + \d y= f(a + \d a, b + \d b, c + \d c, ...)$. A kettő különbsége pedig: $\d y= f(a + \d a, b + \d b, c + \d c, ...) - f(a, b, c, ...)$. Ez az általános képlet.
Elmozdulás mint integrál
Most nézzük egy fordított esetet. Adott egy tárgy sebessége, pl. az autó sebessége az úton az idő függvényében. Matematikailag: $v = f(t)$. Tehát $v$ a sebesség, $t$ az idő. És a sebesség valahogyan függ az időtől ($f$ függvény). A kérdés: Mennyi utat fog megtenni az autó 2 adott időpont között? Mondjuk a 30. másodperc és a 70. másodperc között?
Tegyük fel, hogy az autó a 30. másodpercben 20m/s-mal megy. Akkor a 30. másodpercben 20 m-t tesz meg. A 31. másodpercben mondjuk már 22 m/s-mal megy. Ekkor a 31. másodpercben 22 m-t tesz meg így már 42 méternél tartunk. A 32. másodpercben mondjuk már 24 m/s-mal megy. Ekkor a 32. másodpercben 24 m-t tesz meg így már 66 méternél tartunk. És így tovább, amíg el nem jutunk a 70. másodpercig, és akkor megkapjuk, hogy kb. mennyi utat tett meg.
Matematikailag leírva:
$$ f(t_0)\Delta t + f(t_0 +\Delta t)\Delta t + f(t_0 + 2 \Delta t)\Delta t + ... + + f(t_0 +n \Delta t)\Delta t $$
Vagy röviden:
$$ \sum_{i = 0}^{n} f(t_0 + i \Delta t) \Delta t $$
Ahol $t_0$ az indulási idő, példánkban a 30. másodperc. A $\Delta t$ az esetünkben 1 másodperc, mert másodpercenként néztük. Az $n$ pedig az összeadandó adatok száma, 40 másodperces időintervallumról van szó, amit másodpercenként néztünk, így n = 40/1 = 40. Vagy ha precízebbek akarunk lenni: $n = \frac{t_1 - t_0}{\Delta t}$, ahol $t_1$ a végső időpont tehát a 70.
A kapott összeg kb. annyi, amennyi a helyes megoldás. De mégsem, mert feltételezi, hogy az egyes másodperceken belül változatlan sebességgel haladunk. A sebesség nem a 30. és 31. másodperc között ugrik fel 20-ról 22-re, hanem folyamatosan közben. Ez azt is jelenti, hogy az 1 másodperc alatt megtett távolság kicsit több lesz, mint 20 méter, mert közben gyorsultunk.
Viszont, hogyha 1 másodperces egységek helyett mondjuk egy ezred másodpercekben gondolkodunk, akkor jóval pontosabb eredményt kapunk. A 20 m/s sebességgel haladó autó 1 ezredmásodperc alatt csak 2 centit tesz meg, ez idő alatt, pedig nem igazán tud sokat változni a sebesség, ezért ez már jóval pontosabb. De vannak dolgok, amelyeknél az ezredmásodperc is túl sok. Ott használhatunk mondjuk milliomod másodperces szakaszokat. Minél kisebb szakaszokat adunk össze annál pontosabb lesz az összeg. Így ha matematikailag korrektek akarunk lenni. $\Delta t$-nek picinek kell lennie. Ha pedig $\Delta t$ pici az azt jelenti, hogy $n$ hatamas nagy lesz, mivel a fentebb említett képletben pici dologgal osztottunk. Sok pici sokra megy, így ha végtelenül sok pici dolgot összeadunk, akkor kaphatunk valami emberi lépékkel felfoghatót. És ennek a sok picinek az összeadása az, amiről az integrálás szól. A végtelen sok pici összeadását pedig így jelöljük:
$$ \int_{40}^{70} f(t) \d t $$
Ezt úgy mondjuk, hogy az adott kifejezést integráljuk $t$ szerint 40-től 70-ig. A $\d t$ adja meg, hogy mi szerint integrálunk.

Minél kisebb részeket adunk össze, annál pontosabb eredményt kapunk. Szokták azt is mondani, hogy az integrálással a függvény görbéje alatti területet számoljuk ki. (forrás, szerző, CC-BY-SA)
Newton-Leibniz tétel
Az integrálás és deriválás között szoros kapcsolat áll fenn. Legyen két mennyiségünk $y$ és $x$, köztük valamilyen kapcsolat: $y = F(x)$. Ekkor legyen $f(x) = \frac{\d y}{\d x} = \frac{F(x + \d x) - F(x)}{\d x}$. Tehát van az $F$ függvényünk és annak az $x$ szerinti deriváltja az $f$ függvény. Most integráljuk az $f$ függvényt, mindegy, hogy honnan és meddig (de azért jelöljük a két végpontot $A$-val és $B$-vel) $x$ szerint. Ekkor ahogy az előbb írtuk egy végtelen összegről van szó:
$$ \int_{A}^{B} f(x) \d x = f(A)\d x + f(A + \d x)\d x + f(A + 2\d x)\d x + ... + f(B)\d x $$
Ha behelyettesítünk:
$$ \frac{F(A + \d x) - F(A)}{\d x}\d x + \frac{F(A + 2\d x) - F(A + \d x)}{\d x}\d x + \\ \frac{F(A + 3 \d x) - F(A + 2 \d x)}{\d x}\d x + ... + \frac{F(B + \d x) - F(B)}{\d x}\d x $$
Egyszerűsítjük a törteket:
$$ F(A + \d x) - F(A) + F(A + 2\d x) - F(A + \d x) + F(A + 3 \d x) - \\ F(A + 2 \d x) + ... + F(B + \d x) - F(B) $$
Megfigyelhetjük, hogy az egymást követő tagok szépen kiejtik egymást, mert plusszal és mínusszal is szerepelnek a képletben. Az összegben csak a két szélső tag marad meg, az $F(A)$ és az $F(B + \d x)$, így a fenti összeg egyszerűsödik: $F(B + \d x) - F(A)$. Tehát:
$$ \int_{A}^{B} f(x) \d x = F(B + \d x) - F(A) $$
A $B + \d x$-ben a $\d x$ a B-hez képest elhanyagolhatóan kicsi, így elhagyható és így kapjuk az $F(B) - F(A)$ kifejezést. Hogy mire jó ez? Hogyha egy kifejezésről vagy egy képletről tudjuk, hogy minek a deriváltja, akkor fenti egyszerű képlet alapján tetszőleges tartományában képesek vagyunk összegezni, anélkül, hogy ténylegesen elvégeznénk a végtelen sok összeadást. Ezt úgy mondjuk, hogy $F(B) - F(A)$ az $f(x)$ $x$ szerinti $A$-tól $B$-ig tartó határozott integrálja.
Korábban levezettük a képletet, hogy a szabadon eső test sebessége álló helyzetből kb. $10t$. Ez az $5t^2$ kifejezés, az út képletének, $t$ szerinti deriváltja. Ha tudni akarjuk, hogy pl. ez a labda mennyit esik a 3. és 7. másodperc között akkor csak be kell helyettesíteni: $5(7)^2 - 5(3)^2 = 200$ métert. És nem összeadogatni apránként. Nyilván most annyi előnyünk volt, hogy előre tudtuk a képletet, hiszen először deriváltuk, aztán az alapján elővettük a régi képletet. Viszont ez nem mindig van így. Sőt sokszor nem is lehetséges képlettel kifejezni.
Tegyük fel, hogy $F(x) = x^2 + 45$. Csak példaként. Majd számoljuk ki az $F(B) - F(A)$-t! Csak így paraméteresen: $(B^2 + 45) - (A^2 + 45) = B^2 + 45 - A^2 - 45 = B^2 - A^2$. A konstans tag kiesik.
Tegyük fel, hogy $F(x)$ egy tetszőleges $x$-től függő kifejezés, amelyben van egy konstans tag. Ezt így írhatjuk le szimbólumokkal: $F(x) = g(x) + c$. $c$ a konstans, egy szám. Fejezzük ki az $F(B) - F(A)-t$: $F(B) - F(A) = (g(B) + c) - (g(A) + c) = g(B) + c - g(A) - c = g(B) - g(A)$.
A konstans tag mindig kiesik, amikor határozott integrált számítunk. Erre azért tértem ki, mert amikor meghatározzuk az $F$ függvényt az integrálhoz, annak mindig része lesz egy tetszőleges konstans tag. Ennek a konstans tagnak fontos szerepe van a fizikában, ugyanis az a konstans tag teszi lehetővé a kiinduló állapot választhatóságát.
Gyorsulás
Tehát onnét indultunk ki, hogy volt a hely ($s$) és ezt megadtuk az idő ($t$) függvényében. Tehát $s = f(t)$. Aztán meghatároztuk a sebességet egy adott pillanatban ($v$) az alapján, megnéztük, hogy attól a pillanattól kezdve egy pici idő múlva mennyit mozdul el a test. Minél többet mozdul a pici idő alatt annál gyorsabb. Ehhez az ún. differenciálás módszerét használtuk és így matematikailag leírtuk ezt a mennyiséget $v = \d s / \d t$.
Na most a sebesség sem állandó. Az autó gyorsul, ha beletaposunk a gázba, lassul, ha a fékre nyomunk. Hogyan írhatjuk le a sebesség változását? Hát ugyanúgy, ahogy a sebességgel tettük: megnézzük, hogy egy adott pillanathoz képest picit előremenve az időben mennyit változik a sebesség, és ezt elosztani azzal a pici időtartammal. Tehát a keresett képlet: $\d v / \d t$. A mennyiséget pedig úgy hívják, hogy gyorsulás. Ez pozitív, hogyha az autó gyorsul, negatív ha lassul. Jele $a$.
Most nézzük meg ezt is alaposabban matematikailag. Ha van egy mennyiségünk $x$, annak a kis változása $\d x$. A $\d x$ kis változása ezek szerint $\d \d x$. A $\d \d x$ kis változása ezek szerint $\d \d \d x$. Hogy ne halmozzuk a $\d$-ket összevonjuk, és a $\d \d \d x$ helyett azt írjuk pl., hogy $\d^3 x$, mintha hatvány lenne. Nem az, csak ezzel jelezzük, hogy 3-szor képeztünk differenciált.
A $v$ helyére behelyettesíthetjük a képletét, így kapjuk, hogy:
$$ \frac{\d \left( \frac{\d s}{ \d t} \right)}{\d t} $$
Na most a $\d t$-t a piciny eltelt időtartamot, rögzíthetjük 2 Ugye általános esetben differenciálás után kapjuk, hogy $\d s = f(t + \d t) - f(t)$. Na most ez 1 egyenlet, és van benne 3 változó. Az egyenlet miatt ebből csak 2 lesz szabadon választható. Mi lekötjük a $\d t $-t, a $t$ továbbra is változhat. . Megmondhatjuk, hogy az márpedig ne változzon. Ekkor a konstanssal való szorzás és osztás szabálya érvényesül ezért kihozható a zárójelből:
$$ \frac{\frac{\d^2 s}{ \d t}}{\d t} = \frac{\d^2 s}{\d t^2} $$
És ez a szokás formája a második deriváltnak, tehát, amikor kétszer deriválunk egy mennyiséget, azt így írjuk.
Gravitáció
Korábban levezettük, hogy a szabadon eső test sebességének a képlete $v = 10t$. Ha ezt differenciáljuk, először $v + \d v = 10(t + \d t) = 10t + 10 \d t$. Kivonás után: $\d v = 10 \d t$. Aztán elosztjuk az idő kicsi változásával: $\d v / \d t = 10$. Egy egyszerű konstans szám.
A Föld felszínén a gravitációs gyorsulás átlagosan 9,81 m/s$^2$, azaz kb. 10 m/s$^2$. Ezt a mennyiséget $g$-vel szoktuk jelölni. A dolog szépsége, hogy a gravitációs gyorsulás mértékét szimplán egy egyszerű számmal le lehet írni.
Térbeli mozgások
Most kicsit általánosítsunk. Eddig a mozgások során csak egyirányú mozgásokról beszéltünk. Volt előre meg volt hátra, és ennyi. Viszont a tér, amiben élünk 3 dimenziós. Van jobbra és balra (az X irány), van fel és le (az Y irány), van előre és hátra (a Z irány). Ez 3 irány. Ahhoz, hogy térben megadjunk egy helyet, már nem csak 1, hanem 3 számra van szükségünk. Ez a szám azt mondja meg, hogy mennyit kell egy szabadon választott referenciaponthoz képest jobbra, mennyit felfelé illetve mennyit kell előre menni, hogy eljussunk az adott pontba. A negatív szám azt jelenti, hogy az iránnyal ellentétesen mozgunk, tehát balra, le vagy hátra a referenciaponthoz képest.
Ez a helyet leíró 3 számot 3 betűvel az $x$, $y$ és $z$-vel szokták jelölni. Ha mozgásról van szó, akkor mind a 3 változót az időtől kell függővé tenni:
$$ \begin{array}{rcl} x & = & x(t) \\ y & = & y(t) \\ z & = & z(t) \\ \end{array} \newcommand{\v}[1]{\mathbf{#1}} $$
Érdemes megfigyelni, hogy bevett szokás a változót és a változónak a képletét azonos betűvel jelölni, mert most perpillanat nagyjából mindegy, hogy, miként függenek ezek a változók az időtől.
Mivel most már 3 változóval dolgozunk egyszerre, és mind a hárommal ugyanazt csináljuk, érdemes ezeket a változókat csokorba szedni, ez egyetlen betűvel jelölni. Ez a vektor. Nyomtatásban általában vastaggal szedik, írásban aláhúzzák. Legyen ez a vektor az $\v x$. És legyen: $\v x = (x, y, z)$. Tehát tartalmazza a 3 helyet leíró számot. Esetünkben ez a vektor a helyet jelöli, ezért úgy is nevezik, hogy helyvektor.
Most már van 3 x-ünk egy változó, egy függvény és most már egy vektor is. Addig nincs gond, amíg el tudjuk dönteni, hogy melyikről van szó: $\v x$: az egész vektor, $x(t)$: a függvény kiértékelése $t$ behelyettesítésével, $x$: ugyanaz, mint $x(t)$, mert úgy definiáltuk. A vektorokról azt kell tudni, hogyha (általában) műveleteket végzünk rajtuk, akkor azt a műveletet az összes tagjukon elvégezzük.
Szóval ha vesszük a hely pici megváltozását, amit logikusan úgy fogunk jelölni, hogy $\d \v x$; az azt jelenti, hogy a vektor összes tagjának a differenciáját vettük, tehát $\d \v x = (\d x, \d y, \d z)$.
Aztán, ha ezt elosztjuk az idő pici megváltozásával:
$$ \v v = \frac{\d \v x}{\d t} = \left( \frac{\d x}{\d t}, \frac{\d y}{\d t}, \frac{\d z}{\d t} \right) $$
Akkor is az összes tagot osztjuk el. Ez a vektor írja le a sebességet a térben. A három szám azt mondja meg, hogy a 3 főirányban (jobb-bal, fel-le, előre-hátra), milyen sebességgel haladunk.
Megnézhetjük a sebesség időhöz képesti változását is. Az lesz a térbeli gyorsulás: $\v a = \frac{\d \v v}{\d t} = \frac{\d^2 \v x}{\d t^2}$.
Eldobott tárgyak röppályája
Na most a gravitáció lefelé húz. Így itt ez a gravitációs gyorsulás vektor: $\v a = (0, -g, 0)$.
Az eldobott tárgyaknak szokott lenni kezdősebessége, ezt a 3 fő irányban megadhatjuk, jelöljük ezekkel: $v_x$, $v_y$, $v_z$. Az X és Z irányú sebesség nem változik, mert a gravitáció oldalra nem húz, csak lefelé. A Y irányú komponens pedig folyamatosan és egyenletesen gyorsul lefelé. Azaz, ha $\v a$-t integráljuk, akkor megkapjuk a sebességet: $\v v = (v_x , v_y - g t, v_z)$. Ugye korábban mondtuk az integrálásnál, hogyha egy kifejezést integrálunk, akkor mindig megjelenik egy konstans tag a képletben, amely a kezdőfeltételeket adja meg. Az esetünkben a kezdő feltétel itt most a kezdősebesség. A $v_x$, $v_y$, $v_z$-t választhatjuk bárminek az előbb említett sebességképlet mindig igaz lesz.
A sebességet már tudjuk. Akkor ahhoz, hogy megkapjuk a röppályát, még egyszer integrálnunk kell a $\v v$-t az idő ($t$) függvényében: $\v x = (x_0 + v_x t , y_0 + v_y t - \frac{1}{2}g t^2, z_0 + v_z t)$. It az $x_0$, $y_0$ és $z_0$ a kezdő pozíció. Ismét egy szabadon választható konstans az integrálásnál.
Látható, hogy itt nem konkrét számokkal dobálózunk már régóta, hanem egy olyan általános képletet keresünk, amibe bármit is helyettesítünk be, mindig a helyes választ adja. Írj be bármilyen kezdő pozíciót, adj meg bármilyen kezdősebességet. Add meg az időt, és máris ki tudod számolni, majd számítógéppel kirajzolni, hogy a labda hogyan repül. Ez az absztrakciók erőssége. Ha megadsz egy képletet, amelybe írsz 3-at meg 4-et, akkor az a képlet csak 3-ra és 4-re lesz igaz. De ha megadod tetszőleges $X$-re és $Y$-ra már rögtön az összes lehetséges számra megadtad a képletet.
Ez egy kis ízelítő volt az analízisből, amit fizikai folyamatok (nem csak mozgás) leírására használnak a fizikusok. Későbbiekben szinte mindegyik irományomban előkerülnek majd.