6. Gravitáció
Ebben a részben a világ legmesszebbre ható erejéről lesz szó. Ez a gravitáció. A gravitációs erő egyenesen arányos a vonzó testek tömegével: kétszer, háromszor nagyobb tömegű test 2-3-szor erősebben vonz. És fordítottan arányos a távolság négyzetével: kétszer, háromszor távolabb lévő testek négyszer, kilencszer kisebb erővel vonzzák egymást.
Hogy kezdődött ez az egész? Eleinte Kopernikusz jött rá arra, hogy a bolygók mozgását egyszerűbben meg lehet adni, hogyha feltételezzük, hogy azok a Nap körül és nem a Föld körül keringenek. Később Tycho Brahe végzett rendkívül pontos méréseket a bolygók mozgásáról. Ezeket aztán Kepler használta fel arra, hogy levezesse a 3 róla elnevezett törvényt.
Kepler törvények
A Kepler első észrevétele az volt, hogy megállapította, hogy a Mars pályája ellipszis, és ennek az egyik gyújtópontjában a Nap áll.
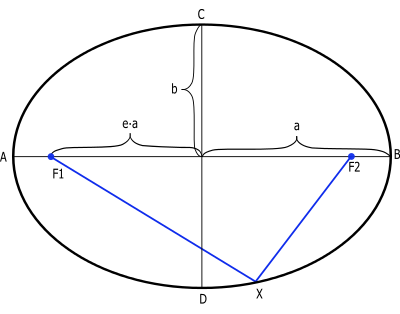
Az ellipszis és részei. Az $a$ a fél nagy tengely. A $b$ a fél kistengely. Az $e$ az excentricitás. forrás
Ellipszist a legegyszerűbben a következő módon lehet rajzolni. Először leszúrunk két szöget. Ezután fogunk egy madzagot, amelynek összekötjük a két végét. A végtelenített madzagot átvetjük a 2 szögön. Majd egy ceruzával a madzagot feszesen tartva körberajzoljuk a 2 szöget. Ha jól csináltuk, akkor egy ellipszist kell kapnunk, amelynek a 2 gyújtópontja (vagy fókuszpontja) a két szög.
Kepler második törvénye az, hogy a Naptól a bolygókhoz húzott vonal azonos idők alatt azonos területet súrol.
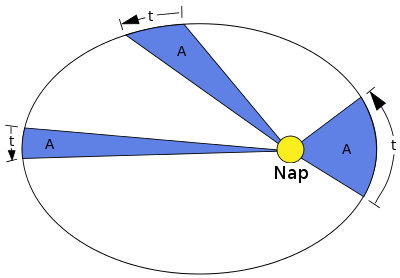
Kepler 2. törvénye (forrás, Szerző, CC-BY-SA AT)
Ahhoz, hogy ez megtörténjen, a bolygónak napközelben gyorsabban kell mennie, mint naptávolban.
A harmadik törvényre majdnem egy évtizeddel korábban jött rá. Ez arról szól, hogy egy bolygó távolságának a köbe egyenes arányban áll a keringési idejének a négyzetével. Tehát, ha egy bolygó 4-szer vagy 9-szer messzebb van a naptól, akkor 8-szor és illetve 27-szer több időbe telik, míg megtesz egy kört. 4-nek a köbe 64, az annyi, mint 8-nak a négyzete. 9-nek a köbe 729, az annyi, mint 27-nek a négyzete.
Bolygók dinamikája
Kepler ugyan rájött néhány törvényszerűségre a bolygók mozgását illetően. De nem tudta levezetni, hogy tulajdonképpen mi is az, ami mozgatja őket. A világban a testeket mozgató szabályokat Newton írta le. Az első törvénye az volt, hogy minden egyes test, egyenes vonalú egyenletes mozgást végez mindaddig, amíg valami más erővel nem hat rá. Ha egy testre erő hat, akkor megváltozik a sebessége. Ha gyorsul, akkor a mozgás irányában hat az erő. Ha lassul, akkor a mozgással ellenkező irányban hat. Ha irányt változtat, akkor a mozgás irányára merőlegesen hat az erő. Vagy ezek kombinációja is lehetséges, hogyha nem irányba vagy merőlegesen, hanem valamilyen köztes irányba mutat az erő.
A mozgás irányában ható erő lassít vagy gyorsít. A rá merőlegesen ható irányt változtat. A kettők kombinációja mindkettőt teszi.
Hogy egy test mozgásállapota mennyire változik meg, az a tömegétől függ. Nehezebb tárgyak mozgásállapotát nehezebb megváltoztatni. 2-szer, 3-szor nehezebb test mozgását, 2-szer, 3-szor lassabb ütemben lehet befolyásolni. Ez az $F = m a$ képlet. Ahol az $F$ az erő, amelynek nagysága és iránya is van, tehát ún. vektormennyiség, és N-ban (newton) mérjük. Az $m$ a tömeg, amit kg (kilogramm-ban). És az $a$ pedig a gyorsulás, amely szintén vektormennyiség, és az erővel egy irányba mutat, ezt $m/s^2$-ben mérjük. A gyorsulás azt mutatja meg, hogy milyen irányban változik a sebesség. Igen a fizikában a gyorsulás nem azt jelenti, hogy az adott tárgy gyorsabb lesz, hanem hogy változik a sebessége, ez van...
Newton gravitációs törvénye
Akkoriban még nem tudták, hogy mi mozgatja a bolygókat. Sokféle fantázia volt arról, hogy miféleképpen mozoghatnak ezek. Pl. hogy angyalok mozgatják őket, vagy hogy valamilyen óraszerkezet hajtja, aminek nem látjuk a fogaskerekeit. Newton Kepler vezérsugaras törvénye alapján gondolta, hogy talán a Napnak köze van a bolygók mozgásához. A keringési periódus és a keringési idő összefüggéséből pedig úgy gondolta, hogy ez a hatás a Naptól távolodva gyengül. Akkoriban már ismert volt, hogy a Jupiter körül holdak keringenek, és az is, hogy a Hold a Föld körül kering. Ekkor Newton eljátszott a gondolattal, hogy a talán a tárgyak közötti erőhatás, a gravitáció, az, amely a pályán tartja a tárgyakat. Akkoriban a Hold távolságát és pályáját nem ismerték kellő pontossággal, ezért Newton is elég pontatlan eredményt kapott, ezért az elméletét félretette. Azonban később pontosabban sikerült megmérni a Hold távolságát, és ekkor a pontosabb adatok ismeretében azt látta, hogy nagyon pontosan meghatározza az elmélete a Hold mozgását. Tehát a bolygók között erő lép fel, amely erő a távolság négyzetével fordítottan arányos, tehát 2, 3-szor távolabbra 4, 9-szer gyengébben hat.
Most nézzük meg, hogy mik a következményei Newton gravitációs törvényének. Ugye a gravitáció itt a Földön egy lefelé ható erő. Bármilyen sebesség szétbontható egy erő irányába ható és egy arra merőleges összetevőre. Az erő csak az erő irányába mutató komponensre hat.
A sebesség felbontható az erő irányába és az erő irányára merőleges összetevőkre a képen látható módon úgy, hogy a sebesség irányát és nagyságát jelképező vektor egy téglalap átlója. A téglalap oldalai pedig az erő irányába, illetve arra merőlegesen állnak. Az erő csak az erő irányába eső komponensre hat, a rá merőlegesre nem.
Ha leejtünk valamit, akkor akkor az az első másodpercben 5 métert esik. És ez független attól, hogy állóhelyzetből esik-e, vagy, hogy van-e vízszintes kezdősebessége neki. Ezt ki lehet próbálni a következő egyszerű kísérlettel. Tegyünk egy rövid vonalzót az asztalra a két végére pedig 2 anyacsavart. Majd így vegyük fel a vonalzót és egyensúlyozzuk az ujjunkon (közben ne essenek le a csavarok). Ezután lökjük le az egyik csavart, hogy nagy sebességgel menjen el oldalra, ekkor a másik is leesik. A két csavar egyszerre fog földet érni.
Két azonos magasságról elejtett test azonos időpontban fog földet érni függetlenül a vízszintes sebességtől.
A leejtett kő és a vízszintesen ellőtt puskagolyó is 5 métert esik az első másodpercben. Csak az a puskagolyó közben azért még halad jó pár száz métert, mielőtt 5 méterrel lentebb kerülne. Viszont ez a Föld nagyjából gömb alakú. Így ha elég nagy a vízszintes sebesség, akkor elég gyorsan mehet az adott tárgy ahhoz, hogy a Föld az 1 másodperces vízszintes útja alatt pont 5 métert görbüljön alatta. Így a tárgy úgy repülhet, hogy nem veszít a magasságából. Tulajdonképpen körbe esik a Föld körül. Így keringenek a holdak és a műholdak a bolygók körül. Így keringenek a bolygók a Nap körül. És minden minden körül.
Ha egy vízszintesen eldobott tárgy elég nagy, akkor az esése pont akkora, amennyire a Föld hajlik alatta. Így habár a pályája hajlik a Föld felé, leesni nem fog: keringeni fog körülötte.
A Pitagorasz-tétel alapján kiszámolható, hogy mennyit kell vízszintesen haladni, hogy Föld annyit görbüljön alattuk, amennyi az esésünk. 1 másodperc alatt a tárgyak 5 métert esnek, ahhoz a Föld 5 métert görbüljön alattunk, 8km-t kell mozogni 1 másodperc alatt.
A Kepler törvények pontosan a két test között ébredő gravitációs erőnek a következményei.
Szintén a gravitációs erő az oka az árapály jelenségnek. A bolygók mozgását fel lehet fogni egy forgómozgásként is, amelyben a gravitációs erő mint egy kötélként húzza a bolygókat egymás felé. Míg a keringésből adódó centrifugális erő eltávolítani igyekszik őket. Ha ez a két erő egyensúlyban van, akkor tökéletes körpálya az eredmény 1Ha kicsit nagyobb sebesség, akkor ellipszis, ha túl nagy, akkor tárgy elszökik a bolygójától. . Na most a centrifugális erő a távolsággal egyenesen arányos. Hogyha egy golyót 2-szer, 3-szor hosszabb madzagon forgatsz a fejed körül másodpercenként egyszer, akkor pályán tartáshoz 2-szer, 3-szor nagyobb erő kell. Viszont a gravitáció a távolsággal négyzetesen húz, 2, 3-szor közelebb van valami; 4, 9-szer erősebb a húzás. Ez azt jelenti, hogy a Holdhoz közeli vízfelület esetén a centrifugális erő gyengébb, mint a gravitációs, ezért ott a víz megemelkedik, ameddig a saját súlya ellent nem áll az erőnek. A Holdtól távolabbi oldalon a centrifugális erő győz a gravitációval szemben, ezért ott meg azért emelkedik meg a víz.
Általános gravitáció
A legtöbb égitest, köztük a Föld is, gömb alakú. Ennek az oka is a gravitációban keresendő. A természetben minden a lehető legkisebb energiaszintre törekszik. A gravitáció esetén a dolgoknak akkor van a legkisebb energiája, hogyha minél lentebb vannak. (Érdemes visszaemlékezni arra, amit a 3. részben írtam a helyzeti energiáról.) A gömb alak pedig az a forma, amelyben minden átlagosan a lehető leglentebb van. Persze a dolgot árnyalja egy picit, hogy a Föld forog, emiatt a legkisebb energiájú állapot nem gömb, hanem az egyenlítőnél valamelyest kidudorodó forgásellipszoid.
A bolygókat nem csak a Nap vonzza, hanem egymást is vonzzák. Csak éppen a Nap a legnagyobb tömegű objektum a Naprendszerben és annak a vonzereje nagyságrendekkel erősebb, mint a többi bolygóé. Viszont a többi bolygó vonzereje nem hanyagolható el teljesen. A bolygóknak mérhető hatása van egymásra. Amikor ezt a hatást is számba vették, még mindig találtak eltéréseket a várt eredményekhez. A bolygók nem pont ott voltak, ahol várták. A Newtoni gravitáció elmélete veszélyben volt. A megfigyelésekből arra következtettek, hogy talán van egy még fel nem fedezett 8. bolygó. Így aztán a 19. század közepén, csupán a gravitációs hatásai alapján, kiszámolták, hogy hol lehet ez a bolygó. Aztán odafordították a távcsövet a kijelölt helyre, és ott volt. Ott a volt a Neptunusz, amely olyan halvány, hogy szabad szemmel már nem látható. De távcsővel nézve is könnyen elveszik hasonlóan halvány csillagok között, ezért nem fedezték fel korábban.
Tehát azt már tudjuk, hogy a gravitáció működik a naprendszeren belül. De működik-e azon kívül? Igen, működik. Vannak kettős csillagok, amelyek egymás körül keringenek. Az ő mozgásukat is pontosan leírja a gravitáció törvénye.
Szintén a gravitáció tartja össze gömbhalmazokat. Ezekben több ezer csillag van, és mivel a csillagok vonzzák egymást, ezért a gravitáció tartja össze őket egy kupacban. Mivel a csillagokat olyan sok helyről húzza a másik csillag, ezért a mozgásuk elég kaotikus. Időnként ki-ki penderül belőlük egy-két csillag. És lassan elfogynak belőlük a csillagok, ez folytatódik mindaddig, amíg csak 2 csillag nem marad, amelyek Kepler-féle ellipszis pályán keringenek egymás körül. Persze ez a dolog nagyon lassan zajlik le.
A galaxisban a csillagok mozgása is a gravitáció törvényeit követi. Sőt a galaxisok mozgása is a gravitáció törvényeit követi.
Szintén a gravitáció okozza, hogy egyáltalán vannak csillagok. Ha a kezdetben főleg hidrogénből álló felhők eléggé lehűlnek, a gravitáció hatására összezuhannak, és csillagok és bolygók alakulnak ki belőlük. Tehát végső soron az is a gravitáció miatt van, hogy létezik Föld és Nap meg a többi bolygó.
Cavendish kísérlet
A gravitáció működik nagyban. Ez tény. De vajon működik-e kicsiben is? Tehát ha fogunk mondjuk 2 ólomgolyót, és közel tesszük egymáshoz, akkor vonzani fogják-e egymást? 1797-ben Cavendish végezte el a kísérletet mely során egy nagyon érzékeny erőmérő műszert alkotott. A dolog lényege az, hogy egy vékony drótra felfüggesztett a közepén egy rudat. A rúd 2 végére pedig rakott egy-egy ólomgolyót. Majd ezen két ólomgolyó közelébe rakott két jóval nehezebb, kb. 160 kg-os, ólomgolyót az átellenes oldalon. Majd megnézte, hogy a rúd mennyire fordul a nehéz ólomgolyók felé. Ahogy a rúd hajlik, a tartó drót csavarodik, és ennek a drótnak van némi ellenállása a csavarodás ellen. Ez állt ellen a golyók között ébredő gravitációs erőnek.
Cavendish meghatározta a csavarodási (torziós) ellenállását, abból, hogy a rákötött rúd a két golyóval milyen gyorsan leng oda és vissza. Tulajdonképpen ez a torziós inga (mert így nevezik hivatalosan), a kísérlet teljes ideje alatt lengett kb. 20 perces periódusidővel. A nagy golyók jelenlétében a kitérés pár milliméteres volt, ahhoz képest, mint amikor nincsenek ott az ólom golyók. De ez már elég volt ahhoz, hogy meghatározzák az arányossági tényezőt a ténylegesen mérhető erő, a tömegek és távolságuk között.
Cavendish-nek sikerült először megmérnie, hogy két adott távolságra lévő adott tömeg között pontosan mekkora gravitációs erő ébred. Ezelőtt ugyan Newton leírta, hogy a gravitációs erő a tömeggel egyenesen, a távolság négyzetével fordítottan arányos, eddig a pillanatig senki sem tudta megmondani, hogy két egymástól 1 méterre elhelyezett 1 kg csomag liszt pontosan mekkora erővel vonzza egymást.
Így jutottunk egy meglehetősen egyszerű törvényszerűséghez, amely a világot nagyban mozgatja:
$$ F = G\frac{m_1 m_2}{r^2} $$
Ahol $F$ a gravitációs erő mértéke. Ahol $m_1$ és $m_2$ két test tömege, $r$ a köztük lévő távolság. A $G$ értéke pedig: $6{,}674 \cdot 10^{-11}$ N m$^2$/kg$^2$. Így ki lehet számolni, hogy két 1 méterre lévő 1 kilós liszt között $6{,}674 \cdot 10^{-11}$ N gravitációs erő ébred.
De talán még fontosabb, hogy a $G$ ismeretében kiszámolható a Föld tömege is. Hiszen ismert, hogy az 1 kg súlyt 9,81 N erővel vonzza a Föld a felszíne közelében, és azt is, hogy a középponttól 6371 km-re vagyunk. A számítás nem nehéz, az olvasóra bízom... Emiatt nevezik a Cavendish kísérletet úgy is, hogy a „Föld tömegének megmérése”.
Mi okozza a gravitációt?
Newton és Cavendish óta pontosan tudjuk, hogy milyen erők mozgatják az égitesteket. Viszont a kíváncsi ember megkérdezheti, hogy mégis mi az oka ennek az erőnek? Mi az oka annak, hogy a tömegek vonzzák egymást?
Rengeteg ötlet felmerült. Az egyik ilyen volt a Le Sage féle gravitációs modell a 18. század közepén (akit érdekel rákereshet). Azonban ez a modell olyan dolgokat is megjósolt, amelyek nem történnek meg a valóságban, valamint nem tudott olyan dolgokat megmagyarázni, amelyek viszont megtörténnek.
Egészen a 20. század elejéig nem volt elméletünk, amely egy szinttel tovább menne és leírná, hogy mi okozza a gravitációt. A dolog egyik szála az volt, hogy a Merkúr mozgása során furcsán viselkedik. Ha kivonjuk a többi bolygó hatását, akkor a pályája elfordul a Nap körül. A Newton törvények szerint ennek nem szabadna megtörténnie. Tehát újabb elmélet kellett, amely kijavítja a Newtoni gravitáció hibáját.
Einstein volt az, aki 1915-ben publikálta az általános relativitáselméletét, amely megoldja ezt a problémát.
Ha bezárunk valakit egy dobozba, akkor nem lehet különbséget tenni aközött, hogy őt most a Föld vonzza-e lefelé gravitációval; vagy egy rakétában ül, amely pontosan $g$-vel, a földi nehézségi gyorsulás mértékével, gyorsul.
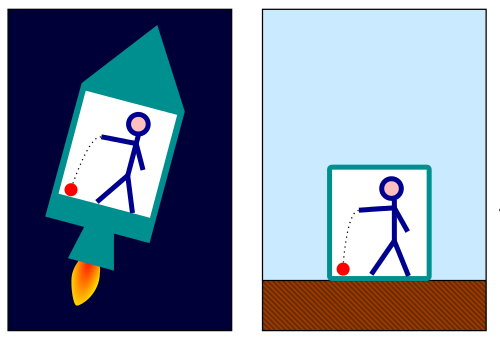
Teljesen mindegy, hogy egy rakéta gyorsul-e veled, vagy a földön állsz. Ha egy dobozba vagy zárva, nem tudod megkülönböztetni a kettőt: pont ugyanúgy esik le a labda mind a két esetben. (forrás, szerző, CC-BY-SA)
Ez volt az alapötlet. Egy olyan elmélet alkotása, amelyben ez a két dolog soha nem különböztethető meg. Mindezt rá kell építeni a korábban leírt speciális relativitásra. Elég kemény matematikai felkészülés kell ahhoz, hogy valaki megértse a matematikáját az általános relativitáselméletnek. Einsteinnek is 10 évig tartott mire sikerült leírnia. Valamint nagyon nehéz felfogni ésszel is, mivel az általános relativitás olyan helyzetekben írja le jól a dolgok menetét, amelyben nagyon nagy sebességek és nagyon nagy tömegek vannak. A Newtoni gravitáció csak kis tömegek és kis sebességek esetén használható jól.
Az általános relativitás lényege az, hogy a tömeg „görbíti a teret”. Ezt úgy szokták elmagyarázni, hogy kifeszítenek egy gumilapot egy keretre vízszintesen. A könnyű golyókat egyenes vonalban lehet átgurítani ezen a lapon. Viszont ha ráraknak egy nehéz vasgolyót, akkor az begörbíti a gumilapot, így a könnyű golyók már nem egyenesen fognak átgurulni rajta, hanem a pályájuk görbül a nagy golyó felé.
Ez egy viszonylag mesterkélt demonstrációja annak, hogy a tömeg hogyan görbíti a teret, és a görbült tér hogyan befolyásolja a testek mozgását. A valóságban kicsit bonyolultabban jön ez ki, a lényeget viszont jól demonstrálja ez a gumilap.
Az általános relativitás lényege, hogy ahol tömeg vagy energia van, ott téridő-görbület is van, és ez okozza a gravitációt. Ezt Einstein téregyenletei írják le, most nem megyünk ebbe bele részletesen, mert nagyon bonyolult. Talán majd később.
Einstein óta ennek az általános relativitásnak szinte az összes következményét sikerült megfigyelni a világegyetemben. Ezek a fekete lyukak, a gravitációs lencse hatás, a gravitációs vörös illetve kékeltolódás, gravitációs hullámok, vagy a bolygók pályájának a precessziója.
Általános relativitás néhány következménye

A fekete lyukaknak olyan erős gravitációja van, hogy még a fény sem szabadul ki belőlük. Ami fény meg éppen elkerüli őket annak is megváltozik az iránya, így érdekes optikai hatásokat keltve. (forrás, szerző, CC-BY-SA)

A közelebbi sárga elliptikus galaxis körül körül elhajlik a mögötte lévő fiatalabb kék galaxis fénye. Emiatt egy gyűrűt látunk a galaxis helyett. (forrás)

Ahogyan a fény távolodik egy nagy tömegű objektumtól, energiát veszít, alacsonyabb frekvenciájú lesz, így valamivel vörösebbé válik. Ez a gravitációs vöröseltolódás. Ez fordítva is igaz. Ha a fény közeledik egy nagy tömegű objektumhoz, energiát nyer, magasabb frekvenciájú lesz, kékebb lesz. (forrás, ismeretlen szerző, CC-BY-SA)