8. Newton dinamikai törvényei
Lendület és erő
Newton előtt nem tudtuk pontosan leírni, hogy hogyan mozognak a dolgok, hogyan mozognak a bolygók, hogyan mozognak a tárgyak. Nem volt jó elméletünk rá. Viszont utána már képesek voltunk leírni a Newton törvények alapján minden hétköznapi mozgást.
Annak idején Galilei határozta meg a tehetetlenség alapelvét: minden test egyenes vonalú egyenletes sebességű mozgást végez, amíg valami meg nem zavarja. Később ez az, amit Newton első törvényeként is ismerünk. A mindennapi életben ezt nehéz demonstrálni, mert minden mozgó testet zavar valami. Pl. a légellenállás vagy a súrlódás előbb vagy utóbb állóra lassít minden testet. Viszont ha nincs levegő, és nincs semmi, ami befolyásolja a testet, akkor az egyenes vonalú egyenletes sebességű mozgást fog végezni.
Newton hozzájárulása az volt a történethez, hogy leírta matematikailag, hogy miként változik meg egy test mozgásállapota. Ez a törvény Newton 2. törvénye.
Mielőtt továbbmennénk először is tisztázni kell fizikailag pár fontos alapfogalmat. A mindennapi életből tudjuk, hogy vannak könnyű és nehéz testek. A könnyű testeket könnyen, kis erővel mozgathatjuk. Míg a nehezeket nagyobb erő megmozgatni. Ez a tulajdonsága a tárgyaknak a tehetetlenség. A tehetetlenség mértéke a tömeg, amit kilogrammban (kg) mérünk. Ez nem összekeverendő a súllyal. A súly azt mondja meg, hogy egy tárgy mekkora erővel nehézkedik rá az azt tartó polcra vagy padlóra. A súly a Holdon a földinek a hatoda, Marson a harmada. Habár a két mennyiség egyenesen arányos, a tömeg mindenhol ugyanannyi, nem változhat meg; a súly változhat a gravitációtól függően. Ugyanúgy nehéz mozgásba hozni a nehéz tárgyakat Holdon és a Marson, mint a Földön. A tömeget általában $m$-mel jelöljük.
A második dolog a lendület. A könnyű test könnyen mozog, a nehéz test nehezebben. Egy nehéz vonat megindításához hatalmas mozdonyoknak kell hatalmas erővel húznia, hogy meginduljon. Szintén több száz fékkel kell egyszerre fékezni, hogy megálljon. Viszont egy hasonló sebességű focilabdát könnyen megállít egy fal. Egy vonat viszont a sebességének a komolyabb megváltozása nélkül áttörne a falon, ha útban lenne. Ez azért van, mert a vonatnak nagyobb lendülete. A lendületet a fizikában úgy kapjuk meg, hogy összeszorozzuk a tömeget a sebességgel. Egy 3 kilós 10 km/h-val repülő medicinlabda ugyanakkorát üt, mint egy fél kilós kislabda, ami 60 km/h-val repül. A lendület jele általában $p$. Képlete ezek szerint $p = mv$, a tömeg és sebesség szorzata. Mértékegysége kg m / s. (kilogramm méter per szekundum).
Ha egy testnek megváltozik a sebessége, akkor megváltozik a lendülete is. A lendület változhat gyorsan vagy lassan. Annak a mértéke, hogy milyen gyorsan változik a lendület, az erő. Matematikailag pedig úgy fejezzük ki, hogy milyen gyorsan változik valami, hogy egy adott időpillanatban megnézzük, hogy egy pillanattal arrébb mennyivel változik a mennyiség. Majd ezt a változást elosztjuk a pillanat hosszával. Azaz:
$$ \newcommand{\d}{\mathrm{d}} \newcommand{\v}[1]{\mathbf{#1}} F = \frac{\d p}{\d t} $$
Mivel előbb írtuk, hogy $p = m v$, így $\d p = \d (m v) = m \d (v)$, mert a konstans kiemelhető, így az előbbi átírható egy másik formába:
$$ F = m \frac{\d v}{\d t} = m a $$
Ebben a másik formában az erő megadja, hogy a test milyen mértékben gyorsul. Ha nagyobb az erő, nagyobb a gyorsulás is. Erősebben taposunk a gázba az autóban, jobban gyorsul. Az erő szokásos jele az $F$. Mértékegysége a newton (N = kg m / s$^2$). Tehát, ha egy 1 kg-os testre 10 N erővel hatunk, akkor az 10 m/s$^2$-tel gyorsul majd.
Fontosnak tartom itt megemlíteni, hogy az erőnek nem csak nagysága van, hanem iránya is. Ugyanis meg lehet mondani, hogy milyen irányba nyom vagy húz az erő. Míg pl. tömegnél vagy időnél nincs értelme arról beszélni, hogy merre 10 kg, vagy merre 30 másodperc.
Sebesség
Az előző részben (a 7. részben) már levezettük a sebességet. Most egy picit részletesebben is belemegyünk. Az angol nyelvben létezik két fogalom a sebességre, a „speed” és a „velocity”. Magyarban sajnos nincs így különvéve a dolog. Így megpróbáljuk körülírni a két dolgot. Pl. ha az irány számít azt mondjuk, hogy sebességvektor, ha nem, akkor azt mondjuk, hogy sebességnagyság.
Fizikában úgy általában, amikor sebességről beszélünk, arra a sebességre gondolunk, amelynek iránya is van. Mivel nem mindegy, hogy milyen gyorsan megyünk, hanem az is számít, hogy merre. Ez az, amire az angol szakirodalom azt mondja, hogy „velocity”. Ha járkálunk a városban, majd hazaérünk, akkor az átlagsebességünk nulla. Mert ugyanabba pontba értünk vissza, ahonnét indultunk, nem volt semmi elmozdulás.
A másikféle sebesség, az, aminek nincs iránya, csak szimplán egy szám, ami megmondja, hogy milyen gyorsan megyünk, ez az, amire az angolok azt mondják, hogy „speed”. Ezt szokták úgy mondani, hogy sebességnagyság. Ezt a számot mutatja a sebességmérő az autóban. Miután megtettünk a városi körutunkat, az átlagos sebességnagyság a megtett út hossza és az eltelt idő hányadosa lesz.
Érdemes megfigyelni itt még egy szóhasználatbeli különbséget. Először azt mondtam, hogy elmozdulás. Ez az elmozdulás egy vektormennyiség, megadja, hogy az érkezési pont milyen messze van a kiindulási ponttól és az irányát is, hogy milyen irányban van az érkezési pont a kiindulásitól. A másik fogalom, amit említettem az út. Ez egy szám, szimplán, amit az autó vagy bicikli kilométerórája mutat. Hogy mekkora távolságot tettük meg, függetlenül a kiindulási és ékezési ponttól. Nem mindegy.
Matematikailag a térbeli sebesség megadható 3 számmal, hogy milyen gyorsan megyünk előre, jobbra és felfelé. Nyilván ha átlósan mozgunk, akkor mind a három irányban lehet nullánál nagyobb sebességünk. Tehát legyen $\v v = (v_1, v_2, v_3)$, tetszőleges sebesség. Egy piciny idő alatt megtett elmozdulás $\v v \d t = (v_1 \d t, v_2 \d t, v_3 \d t)$ lesz.
Kis elmozdulás ábrázolása. Az átlós irányban haladó test mind a három irányban halad egyszerre. Valahogy így kellene elképzelni, a sebesség 3 komponensét.
Adott a piciny elmozdulás. Mennyi lesz az út? A fentebb mutatott geometriai helyzet alapján ezt Pitagorasz tétellel kiszámolhatjuk. Vesszük a négyzetösszegét az egyes elmozdulásoknak, majd gyököt vonunk belőle:
$$ \sqrt{v_1^2 \d t^2 + v_2^2 \d t^2 + v_3^2 \d t^2} = \d t \sqrt{v_1^2 + v_2^2 + v_3^2} $$
A $\sqrt{v_1^2 + v_2^2 + v_3^2}$ rész a sebesség nagysága, egy szám. Ez a „speed”, amit megkaphatunk a „velocity”-ből így. Ezt $\d t$-vel beszorozva kapjuk a kis utat. Úgy általában egy vektormennyiség nagyságát úgy jelöljük, hogy az abszolút értékbe tesszük így: $|\v v| = \sqrt{v_1^2 + v_2^2 + v_3^2}$. Tehát így jelöljük a sebesség nagyságát. Ami az abszolút értéket illeti, az analógia adott. Az abszolút érték egy szám nullától való távolságát jelenti. A -4 és 4-re; 4 is 4-re van a nullától. Vektorok esetén a nullától való távolságot úgy lehet elképzelni, hogy vektorban lévő 3 számot ábrázoljuk 3 dimenziós koordináta-rendszerben, és akkor az origótól való távolság egy vektor abszolút érték.
Van olyan is, amikor egy vektormennyiségnek az irányára vagyunk csak kíváncsi. Ilyenkor elosztjuk a vektort a nagyságával: $\v v / | \v v |$. Az így kapott vektor nagysága 1 lesz, az iránya pedig megegyezik az eredeti vektorral. (házi feladat leellenőrizni, hogy miért. :)
Sebesség, gyorsulás és erő összetevői
Ugye a sebességvektornak 3 része szokott lenni: $\v v = (v_1, v_2, v_3)$. Azt mondtuk az előző részben (a 7. részben), hogyha egy vektorral műveletet végzünk, akkor minden elemével műveletet végzünk. Ha megszorozzuk a mozgó test sebességét a tömeggel: $\v p = m \v v = (m v_1, m v_2, m v_3)$ megkapjuk a lendület vektort. A lendület változásának a gyorsasága az erővektor lesz: $\v F = m \frac{\d v}{\d t} = (m \frac{\d v_1}{\d t}, m \frac{\d v_2}{\d t}, m \frac{\d v_3}{\d t})$.
Látható, hogy a 3 főirány mentén bekövetkező gyorsulások függetlenek egymástól. Az erő X irányú komponense az X irányban gyorsít csak. Az Y irányú az Y irányban. A Z a Z-ben. Az X irányú komponens nem szól bele az Y és Z irányúba. Ahogyan az Y sem az X és Z-be. Illetve a Z komponens sem X és Y-ba.
Az előző szekcióban láttuk, hogy a sebességvektor tényleges nagysága és iránya hogyan határozható meg 3 komponens segítségével. Most nézzük meg a fordított helyzetet: adott, hogy merre megy a tárgy, és adott, hogy milyen gyorsan megy. Hogyan határozhatjuk meg ebből a komponensek nagyságát?
Először is, ha a két karunkkal mutatunk 2 különböző irányba, akkor megmérhetjük ezen 2 irány által bezárt szöget. Tehát bármilyen 2 irány esetén értelmezhető a köztük bezárt szög.
Na most legyen adott a 3 egymásra merőleges fő irány. Hogy megkapjuk, hogy egyes irányokban mekkora sebesség, vegyük a sebesség iránya és a főirányok által bezárt szöget. Vegyük ennek a szögnek a koszinuszát, és szorozzuk be a sebesség nagyságával. Így megkapjuk, hogy az adott főirányban mekkora a sebesség. Hogy jobban el lehessen képzelni itt egy rajz erről:
Ha adott egy vektor nagysága és iránya, akkor az ábrán látható geometriai módon határozhatóak meg a komponensei az egymásra merőleges főirányokban.
Mozgás törvényei
Ha valami gyorsul, akkor ott erő is van. De mi határozza meg, hogy mekkora ez az erő úgy általában? Mi írja le a mozgás szabályait?
Ilyen pl. a gravitációs erő a Földön: $F = mg$. Ez esetünkben egy állandó lefelé húzó erő, amely nagyjából független a helyünktől. Ez egy egyszerű mozgási szabály. De ez nem mindig van így. Nézzünk pl. egy rúgót. A rúgóról azt kell tudni, hogy minél inkább széthúzod, annál nagyobb erővel húz vissza. Képlettel leírva: $F = -kx$. Ahol $F$ az erő, amennyire húz. A $k$ a rúgó keménységét jellemző szám. Az $x$ az elmozdulás mértéke. Amikor $x$ nulla, akkor a rúgó nem húz semerre. Amikor $x$ negatív, akkor a rúgót összenyomtuk, ezért visszafelé nyom. Amikor $x$ pozitív, akkor széthúztuk a rúgó, ekkora visszafelé húz.
Az előzőt valahogy így kell elképzelni. Egy rúgón lógatunk egy tárgyat. A pont, ahol a test nyugalomban van legyen az $x = 0$ pont. Ha lentebb húzzuk, ott $x$ pozitív, ha fentebb nyomjuk, akkor ott $x$ negatív legyen. Hasonlóképpen, hogyha a test lefelé mozog, akkor a sebessége pozitív, ha felfelé, akkor negatív.
Na most tegyük fel, hogy a rúgóra kötünk egy valamilyen $m$ tömegű testet. Ekkor ugye az $F = ma$ törvényből adódóan a rúgó mozgástörvénye a következőképpen módosul: $m a = -k x$.
Vegyük az alaphelyzetet, a testet ráakasztjuk a rúgóra és békén hagyjuk. Ekkor a rúgó abban a helyzetben áll, amikor nem nyom és nem húz. Nem mozgatja a testet semerre. Ekkor $a = 0$ nincs mozgás, nincs gyorsulás.
Mi történik, ha lehúzzuk a testet, és elengedjük? Ugye tudjuk, hogy $a = \frac{\d^2 x}{\d t^2}$. Így a fenti képlet a következővé alakul át:
$$ m \frac{\d^2 x}{\d t^2} = -k x $$
A gyorsulás függ attól, hogy a test éppen hol van a rúgón. Egy mennyiség változásának az üteme függ magától a mennyiségtől. Ez egy ún. differenciálegyenlet, amely egy mennyiség és annak változása között teremt kapcsolatot. A példánkban ez a mennyiség az $x$. Ez egy dinamikai egyenlet, vagy úgy is mondják, hogy a mozgás egyenlete.
A mozgás egyenleteinek az értelme
A mozgás egyenleteinek, mint a fenti példában a rúgó egyenlete, segítségével pontosan meghatározható, hogy egy test vagy egy komplett rendszer hogyan fog változni az idő múlásával. Ebben a szekcióban ezt nézzük meg kicsit bővebben.
A dolog onnét indul, hogy van egy mennyiségünk $x$. Amely az idő függvényében változik: $x = x(t)$. $t$ az idő.
A $t$ pici változása, pici változást idéz elő a $x$ mennyiségben is. Ezt úgy jelöltük, hogy: $x + \d x = x(t + \d t)$.
Na most elkövetünk egy kis algebrai trükköt, melynek során osztunk és szorzunk $\d t$-vel: $\d x = \frac{\d x}{\d t} \d t$. Ettől nem fog változni az érték. Ebből a $\d x / \d t = v = v(t)$, azaz $v$ a sebesség a $t$ időpontban, illetve definiáltunk egy $v$ függvényt is, amellyel megadhatjuk a sebességet bármely időpontban. Így az egyenletünk most perpillanat:
$$ x(t + \d t) = x(t) + v(t) \d t $$
A mozgó tárgy, mint pl. egy autó, egy pici idő múltával annyival lesz előrébb, mint amennyi a sebessége szorozva ezzel a piciny időtartammal. Semmi új nincs ebben.
Ugyanezt, amit előbb az $x$-szel játszottunk el pontosan ugyanígy eljátszhatjuk a $v$-vel is. És kapjuk ezt az egyenletet:
$$ v(t + \d t) = v(t) + a(t) \d t $$
A tárgy sebessége annyival változik meg a pici idő alatt, amennyi a gyorsulása szorozva ezzel a pici időtartammal.
Ahol $a = \d v / \d t = a(t)$. Tehát a gyorsulás egy adott időpontban.
Mit ír le ez a két egyenlet? Azt, hogyha egy picikét előremegyünk az időben, mennyit változik a sebesség és a hely. Na és itt jön a képbe a mozgás egyenlete: $m a = -k x$. $m$-mel leosztjuk mind a két oldalt, hogy kapjuk, hogy $a = -\frac{k}{m}x$. A test tömege, az $m$, és a $k$ állandók, nem változnak. Így összevonhatnánk a $k/m$-et egyetlen egy betűbe: $K = k/m$. Így az egyenletünk egyszerűbb lesz: $a = -K x$.
Na most ezt az $a$ és az $x$ közötti, a gyorsulás és a hely közötti, összefüggést tegyük be az egyenleteinkbe:
$$ x(t + \d t) = x(t) + v(t) \d t \\ v(t + \d t) = v(t) - K x(t) \d t $$
Láthatjuk, hogy az $a$-t lecseréltük benne. Hogy ebben mi a jó? Ha adott a test helye és sebessége, akkor kiszámolhatjuk, hogy egy pici idő múlva mi lesz a test helye és sebessége. Aztán megint és megint. A képlet ott van fentebb. Manapság egy számítógépes programmal elvégezhető ez, és elkészíthető egy animáció a mozgásról.
Mozgás egyenletének a megoldása
Előbb felírtuk, hogy hogyan kell értelmezni a mozgás egyenletét. És elmondtuk, hogy a segítségével számítógépes szimuláció is készíthető. Viszont ezzel a két egyenlettel van egy kis probléma: a $\d t$ nagyon pici; nagyobb, mint nulla, de kisebb mint bármilyen pozitív szám, így abban a formában nem használható. Végtelenül pici időtartamokkal nem tudunk számolni, de számolhatunk kicsi időtartamokkal, mint pl. 0,1 másodperccel. Tehát visszatérünk a deltákhoz, amiből kiindultunk az előző fejezetben: legyen $\Delta t = 0{,}1$. Így az egyenletek már csak közelítőleg lesznek igazak:
$$ x(t + \Delta t) \approx x(t) + v(t) \Delta t \\ v(t + \Delta t) \approx v(t) - K x(t) \Delta t $$
Nézzük, hogy ez hogy néz ki gyakorlatban. A kiinduló időpont legyen $t = 0$. Húzzuk le a testet mondjuk 1 méterrel, tehát $x(0) = 1$. És ebben a pontban álljon a test $v(0) = 0$. Legyen $K = 1$ az egyszerűség kedvéért. És legyen $\Delta t = 0{,}1$, ahogy előbb írtuk.
Így behelyettesítés után az első lépés után a 0,1. másodpercben a következő az állás:
$$ x(0{,}1) \approx 1 + 0 \cdot 0{,}1 = 1\\ v(0{,}1) \approx 0 - 1 \cdot 1 \cdot 0{,}1 = -0{,}1 $$
A következő lépés után:
$$ x(0{,}2) \approx 1 - 0{,}1 \cdot 0{,}1 = 0{,}99 \\ v(0{,}2) \approx -0{,}1 - 1 \cdot 1 \cdot 0{,}1 = -0,2 $$
És innentől igazából Excellel (vagy LibreOffice Calc-cal vagy C programmal vagy amivel akarod) lehet folytatni a dolgot, és kapjuk a következő táblázatot a mozgásra:
| t | x | v |
|---|---|---|
| 0 | 1 | 0 |
| 0,1 | 1 | -0,1 |
| 0,2 | 0,99 | -0,2 |
| 0,3 | 0,97 | -0,299 |
| 0,4 | 0,9401 | -0,396 |
| 0,5 | 0,9005 | -0,49001 |
| 0,6 | 0,851499 | -0,58006 |
| 0,7 | 0,793493 | -0,6652099 |
| 0,8 | 0,72697201 | -0,7445592 |
| 0,9 | 0,65251609 | -0,817256401 |
| 1 | 0,5707904499 | -0,88250801 |
| 1,1 | 0,4825396489 | -0,939587055 |
| 1,2 | 0,3885809434 | -0,9878410199 |
| 1,3 | 0,2897968414 | -1,0266991142 |
| 1,4 | 0,18712693 | -1,0556787984 |
| 1,5 | 0,0815590502 | -1,0743914914 |
| 1,6 | -0,025880099 | -1,0825473964 |
| 1,7 | -0,1341348386 | -1,0799593865 |
| 1,8 | -0,2421307773 | -1,0665459026 |
| 1,9 | -0,3487853675 | -1,0423328249 |
| 2 | -0,45301865 | -1,0074542881 |
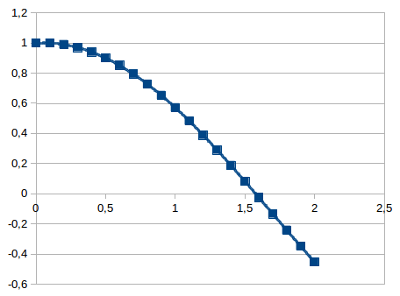
$x$ ábrázolása $t$ függvényében.
Itt már látunk valamiféle szimulációszerűt. De már az első lépésnél látunk valami furcsát. Az első tizedmásodpercben a tárgy sebessége -0,1 lesz tehát a rúgó elkezdi a testet visszahúzni. Viszont a helye még sem változott meg, 1 maradt. Nyilvánvaló, hogy nem jöhet mozgásba valami úgy, hogy közben nem mozdul meg. Tehát a szimulációnk nem elég pontos.
A probléma oka az, amiért is $\approx$ jelet használtunk. A tizedmásodperces időtartam alatt maga az $x$ és a $v$ is már változik. Viszont mi ezt nem vettük figyelembe, úgy számoltunk, hogy nem változik. A tizedmásodperces időtartam már nem végtelenül kicsi, mint a $\d t$, ezért most már nem gondolhatunk a sebességre úgy, mint ami ezen kis idő tartam alatt nem változik. Jelenleg a számolásunk szerint a sebesség lényegében a tizedmásodperces időtartam végén ugrik -0,1-re. Ez nem megfelelő.
Számolnunk kell azzal, hogy a tárgy sebessége változik a tizedmásodperc alatt. Tételezzük fel, hogy a tárgy sebességének a változása egyenletes. Kérdés: mennyi utat tesz meg a tárgy, egy adott idő alatt miközben egyenletesen változik a sebessége?
Már foglalkoztunk egyenletesen változó sebességgel az előző fejezetben. Ez volt a szabadesés. A szabadon eső test sebessége folyamatosan növekszik, ahogy esik lefelé. A szabadon eső test gyorsulása $g$ a gravitációs gyorsulás. A sebessége álló helyzetből való indulás után $t$ idővel $gt$. A megtett út pedig álló helyzetből indulás után $t$ idővel $gt^2 / 2$.
Na most nézzünk két időpontot, egy tetszőleges $t_1$ időpontban a szabadon eső test sebessége $g t_1$, jelöljük ezt $v_1$-gyel. Megtett útja $gt_1^2 / 2$, jelöljük ezt $s_1$-gyel. Később egy tetszőleges $t_2$ időpontban a szabadon eső test sebessége $g t_2$, jelöljük ezt $v_2$-vel. Megtett útja $gt_2^2 / 2$, jelöljük ezt $s_2$-vel.
A $t_1$ és $t_2$ között eltelt idő $t_2 - t_1$, jelöljük ezt $\Delta t$-vel. A két időpont között megtett út:
$$ \frac{gt_2^2 - gt_1^2}{2} $$
Emeljük ki a $g$-t:
$$ g\frac{t_2^2 - t_1^2}{2} $$
Alkalmazzuk ezt az azonosságot: $x^2 - y^2 = (x+y)(x-y)$, mely igaz tetszőleges $x$ és $y$ számokra.
$$ g\frac{(t_2 + t_1)(t_2 - t_1)}{2} $$
Helyettesítsük be a $\Delta t$-t a $t_2 - t_1$ helyére, és emeljük ki:
$$ g \frac{t_2 + t_1}{2} \Delta t $$
A $\frac{t_2 + t_1}{2}$ tényezőben a $t_2$-t be lehet helyettesíteni $t_1 + \Delta t$-vel. Így kapjuk azt, hogy $\frac{2 t_1 + \Delta t}{2}$, amely egyenlő: $t_1 + \frac{\Delta t}{2}$-vel. Tehát ez az időpont pontosan a két adott időpont között félúton van. Ez be van szorozva $g$-vel tehát, a $g \frac{t_2 + t_1}{2}$ a sebesség az időtartam közepén. És ez van beszorozva $\Delta t$-vel, hogy megkapjuk az utat.
És kész vagyunk azzal, amire ki akartam lyukadni. Ha egyenletesen változik a sebesség egy időtartamban, akkor a megtett úthoz az időtartam közepén mért sebességet kell venni. Akkor most a kitérő után térjünk vissza az eredeti egyenleteinkhez és annak a jelöléseihez. Most már pontosabb szimulációt csinálhatunk:
$$ x(t + \Delta t) \approx x(t) + v(t + \Delta t / 2) \Delta t \\ $$
Na most, amit a hellyel és a sebességgel játszottunk el, eljátszhatjuk a másik egyenlettel is. A $v(t + \Delta t / 2)$-t az egy lépéssel korábbi $v(t - \Delta t / 2)$-hez viszonyítva számoljuk ki. Itt is feltételezzük, hogy a gyorsulás egyenletesen változik, így a pontosság kedvéért itt is időben a fél úton lévő értéket kell venni. Ami nekünk pont jó, mert pont az $a(t)$ van fél úton. Így a másik egyenlet:
$$ v(t + \Delta t / 2) \approx v(t - \Delta t / 2) + a(t) \Delta t $$
Az $a(t)$ helyére pedig, ahogy előbb tettük be helyettesítjük $- K x(t)$-t. Így az új egyenletek együtt, amivel szimulálni fogunk:
$$ x(t + \Delta t) \approx x(t) + v(t + \Delta t / 2) \Delta t \\ v(t + \Delta t / 2) \approx v(t - \Delta t / 2) - K x(t) \Delta t $$
Most viszont nem tudjuk még, hogy mennyi a $v(t - \Delta t / 2)$. Tehát a kiinduló sebesség a -0,05 másodpercnél. Ennek a megbecsüléséhez a kiinduló $v(t + \d t) = v(t) - K x(t) \d t$ egyenletet használhatjuk, melyben a $\d t$ helyére $- \Delta t / 2$-t helyettesítünk:
$$ v(t - \Delta t / 2) \approx v(t) + K x(t) \Delta t / 2 $$
Vagyis:
$$ v(-0{,}05) \approx v(0) + x(0) 0{,}05 = 0{,}05 $$
Így az első körben a sebesség és az elmozdulás:
$$ v(0 + 0{,}05) \approx v(0 - 0{,}05) - 1 x(0) 0{,}1 = 0{,}05 - 1 \cdot 1 \cdot 0,1 = -0{,}05 \\ x(0 + 0{,}1) \approx x(0) + v(0 + 0{,}05) 0{,}1 = 1 -0{,}05 \cdot 0{,}1 = 0{,}995 $$
A következő lépésben:
$$ v(0{,}15) \approx v(0{,}05) - 1 x(0{,}1) 0{,}1 = -0{,}05 - 1 \cdot 0,995 \cdot 0,1 = -0{,}1495 \\ x(0{,}2) \approx x(0{,}1) + v(0{,}15) 0{,}1 = 0,995 -0{,}1495 \cdot 0{,}1 = 0{,}98005 $$
És így tovább. Excel segítségével ki lehet számolni gyorsan, sok lépés eredményét:
| $t$ | $x$ | $v$ |
|---|---|---|
| -0,05 | 0,05 | |
| 0 | 1 | |
| 0,05 | -0,05 | |
| 0,1 | 0,995 | |
| 0,15 | -0,1495 | |
| 0,2 | 0,98005 | |
| 0,25 | -0,247505 | |
| 0,3 | 0,9552995 | |
| 0,35 | -0,34303495 | |
| 0,4 | 0,920996005 | |
| 0,45 | -0,4351345505 | |
| 0,5 | 0,87748255 | |
| 0,55 | -0,5228828055 | |
| 0,6 | 0,8251942694 | |
| 0,65 | -0,6054022324 | |
| 0,7 | 0,7646540462 | |
| 0,75 | -0,6818676371 | |
| 0,8 | 0,6964672825 | |
| 0,85 | -0,7515143653 | |
| 0,9 | 0,6213158459 | |
| 0,95 | -0,8136459499 | |
| 1 | 0,5399512509 | |
| 1,05 | -0,867641075 | |
| 1,1 | 0,4531871434 | |
| 1,15 | -0,9129597893 | |
| 1,2 | 0,3618911645 | |
| 1,25 | -0,9491489058 | |
| 1,3 | 0,2669762739 | |
| 1,35 | -0,9758465332 | |
| 1,4 | 0,1693916206 | |
| 1,45 | -0,9927856952 | |
| 1,5 | 0,0701130511 | |
| 1,55 | -0,9997970003 | |
| 1,6 | -0,0298666489 | |
| 1,65 | -0,9968103354 | |
| 1,7 | -0,1295476825 | |
| 1,75 | -0,9838555672 | |
| 1,8 | -0,2279332392 | |
| 1,85 | -0,9610622433 | |
| 1,9 | -0,3240394635 | |
| 1,95 | -0,9286582969 | |
| 2 | -0,4169052932 |
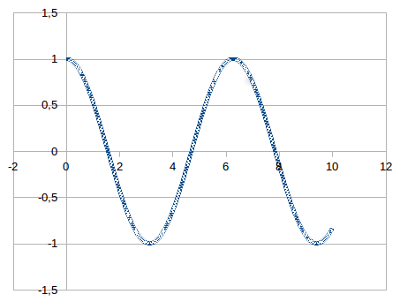
$x$ ábrázolása $t$ függvényében. Az első 10 másodpercben. Immár a javított képlet használatával. Látható, hogy a rúgóra rakott test fel-le mozog. A valóságban csillapított a rezgés, így az amplitúdó az idővel csökken. A mi esetünkben viszont nincs csillapítás így folyamatosan rezeg a test.
Ebben a szekcióban megnéztük, hogy hogyan lehet a mozgást leíró egyenletek alapján lépésenként kiszámolni magát a mozgást. Viszont a rúgóra akasztott tárgy mozgását leíró egyenlet az $a = -Kx$ azon ritka egyenletek közé tartozik, amelynek van analitikus megoldása is. Ez azt jelenti, hogy az egy adott időpontban a sebesség és a hely meghatározható egy képletbe való behelyettesítéssel is. Nem szükséges lépésekkel végigszimulálni. Ez pedig az $x(t) = c_1 \mathrm{cos}(\sqrt{K} t) + c_2 \mathrm{sin}(\sqrt{K} t)$. Ahol a $c_1$-et és $c_2$-t a kezdőfeltételek alapján lehet meghatározni. Esetünkben: $c_1 = x(0)$. $c_2 = v(0) / \sqrt{K}$. Direkt azért választottam a $v(0)$-t 0-nak, az $x(0)$-t 1-nek, a $K$-t szintén 1-nek, hogy az egész képlet leegyszerűsödjön erre: $x(t) = \mathrm{cos}(t)$. Ez az egyszerű koszinusz függvény.
Érdemes összevetni ezt a képletet az előző lépésenként kapott táblázattal. Érdemes kipróbálni azt is, hogy mennyivel leszünk pontosabbak, hogyha a $\Delta t$-t kisebbnek mondjuk 0,01-nek választjuk (ha Excelben jól csináltuk, csak egy cellát kell átírni). A lépésenként a hiba nagyságrendje $\Delta t$ négyzetével arányos, minél kisebbnek választjuk, annál pontosabb lesz a szimulációnk.
Bolygók mozgása
A 6. részben írtam a gravitációról. Ott felírtuk, hogy a gravitációs erő nagysága a következő:
$$ F = G \frac{m M}{r^2} $$
Az $M$ a nehezebb test tömege (pl. a Nap), az $m$ a könnyebbé (pl. a bolygó), az $r$ pedig a távolságuk, a $G$ a gravitációs konstans, az $F$ pedig a köztük fellépő erő. Nézzük meg, hogyha ez alapján szimulációt készítünk, akkor kijön-e a bolygók ellipszis pályája!
A kisebbik test gyorsulását $m$-el elosztva kapjuk meg:
$$ a = \frac{G M}{r^2} $$
A nagyobb tömegű testé pedig $\frac{G m}{r^2}$, ott az $M$-el osztottuk le. Tételezzük fel, hogy a kisebb test tömege nagyon pici. Így az általa okozott gravitációs hatás is elhanyagolhatóan kicsi (és nem fogja mérhetően rángatni a Napot).
A koordináta-rendszerünkben legyen a Nap az origóban. Na most a gyorsulás nagyságát már tudjuk. Ott van az előző képletben. Mi a helyzet az irányával? Ha a tárgy a Naptól jobbra van, akkor balra húzza; ha balra van tőle, akkor jobbra húzza; ha felette van, akkor lefelé húzza; ha alatta, akkor felfelé húzza. Tehát a gyorsulás iránya ellenkezője lesz a bolygó irányának a Naphoz képest.
Matematikailag kifejezve:
$$ \frac{\v a}{|\v a|} = - \frac{\v r}{|\v r|} $$
Az $\v a$ a gyorsulás vektora (3 szám) az $\v r$ pedig a mozgó test helye a térben (szintén 3 szám). Ahogy korábban említettük, amikor egy vektort elosztunk a nagyságával, akkor egy azonos irányú, de 1 hosszúságú vektort kapunk. Ez alkalmas két vektormennyiség irányának az összehasonlítására. A negatív előjel a vektor előtt megfordítja a vektor irányát. Így fejeztük ki, hogy a gyorsulás iránya és a hely iránya ellenkező lesz.
Na most akkor játsszunk ezzel az egyenlettel, először vigyük át a gyorsulás nagyságát (szorozzuk vele mind a két oldalt):
$$ \v a = - \frac{\v r |\v a|}{|\v r|} $$
És akkor helyettesítsük is be a gyorsulás nagyságának a képletét (majd egyszerűsítsünk):
$$ \v a = - \frac{\v r G M}{|\v r|^3} $$
És ez a bolygómozgás egyenlete. Itt most nem csak 1 darab számról van szó, hanem 3-ról, egyetlen egyenletben. Mert ugye az előző fejezetben mondtuk, hogy a vektorokkal végzett művelet olyan, amit az összes tagra értelmezünk. Így az előző egyenletet szét is bonthatjuk a tagonkénti egyenletekre, ha úgy tetszik:
$$ a_1 = - \frac{G M}{|\v r|^3}r_1 \\ a_2 = - \frac{G M}{|\v r|^3}r_2 \\ a_3 = - \frac{G M}{|\v r|^3}r_3 $$
Most jogos lehet a kérdés, hogy a $|\v r|$-t mért nem bontottuk szét? A válasz az: mert az egy szám, a vektor nagysága. A számokat békén hagyjuk, csak a vektorokat szedjük szét.
Na most itt van 3 mozgás egyenlet. Tételezzük fel, hogy a Nap és a bolygó is a képernyő síkjában van. Ekkor a gyorsulás is a képernyő síkjában lesz, így a test nem fog tudni kimozdulni a képernyő síkjából. Így a 3. koordináta 0 marad. Így a harmadik egyenlettel nem is kell foglalkoznunk.
Az első kettővel viszont kell. Egyszerre. Úgy kell, ahogy a rúgónál is tettük, ugyanaz a játék. Fel kell írni a lépéseknél használt egyenletet, és behelyettesíteni a gyorsulás képletét:
$$ r_1(t + \Delta t) \approx r_1(t) + v_1(t + \Delta t / 2) \Delta t \\ v_1(t + \Delta t / 2) \approx v_1(t - \Delta t / 2) - \frac{G M}{|\v r(t)|^3} r_1(t) \Delta t \\ r_2(t + \Delta t) \approx r_2(t) + v_2(t + \Delta t / 2) \Delta t \\ v_2(t + \Delta t / 2) \approx v_2(t - \Delta t / 2) - \frac{G M}{|\v r(t)|^3} r_2(t) \Delta t $$
Ahol $r_1(t)$, $r_2(t)$ a bolygó helyének 2 koordinátája $t$ időpontban. A $v_1(t)$, $v_2(t)$ a vízszintes és függőleges sebesség egy adott $t$ időpontban. Az $\v r(t)$ pedig az $r_1(t)$ és az $r_2(t)$ összevonva egybe.
Na most akkor mi legyen a kezdőállapot. Először is az $M$-et válasszuk úgy, hogy a $GM = 1$ legyen. Az egyszerűség kedvéért. Az idő lépései legyen mondjuk $\Delta t = 0,1$. Tehát ismét tizedmásodperc. A kezdőhely legyen mondjuk: $\v r(0) = (5; 0)$. Tehát a naptól jobbra 5 egységnyire. A sebesség pedig legyen mondjuk: $\v v(0) = (0; 0,4)$. Tehát felfelé mozogjon a test az induláskor.
Tehát akkor számoljuk ki a pályát. A következő táblázat jön össze:
| $t$ | $r_1$ | $v_1$ | $r_2$ | $v_2$ | $|\v r|$ |
|---|---|---|---|---|---|
| -0,05 | 0,002 | 0,4 | |||
| 0 | 5 | 0 | 0 | 0,4 | 5 |
| 0,05 | -0,002 | 0,4 | |||
| 0,1 | 4,9998 | 0,04 | 4,9999600038 | ||
| 0,15 | -0,005999936 | 0,3999679992 | |||
| 0,2 | 4,9992000064 | 0,0799967999 | 4,9998400166 | ||
| 0,25 | -0,0099996799 | 0,3999039956 | |||
| 0,3 | 4,9982000384 | 0,1199871995 | 4,9996400422 | ||
| 0,35 | -0,0139991037 | 0,3998079852 | |||
| 0,4 | 4,996800128 | 0,159967998 | 4,9993600871 | ||
| 0,45 | -0,017998079 | 0,3996799616 | |||
| 0,5 | 4,9950003201 | 0,1999359942 | 4,99900016 | ||
| 0,55 | -0,0219964774 | 0,3995199168 | |||
| 0,6 | 4,9928006724 | 0,2398879858 | 4,9985602727 | ||
| 0,65 | -0,0259941703 | 0,3993278406 | |||
| 0,7 | 4,9902012554 | 0,2798207699 | 4,9980404393 | ||
| 0,75 | -0,0299910287 | 0,3991037205 | |||
| 0,8 | 4,9872021525 | 0,319731142 | 4,9974406763 | ||
| 0,85 | -0,0339869234 | 0,3988475424 | |||
| 0,9 | 4,9838034602 | 0,3596158962 | 4,9967610031 | ||
| 0,95 | -0,0379817246 | 0,3985592899 | |||
| 1 | 4,9800052877 | 0,3994718252 | 4,9960014416 | ||
| 1,05 | -0,0419753023 | 0,3982389445 | |||
| 1,1 | 4,9758077575 | 0,4392957196 | 4,9951620163 | ||
| 1,15 | -0,0459675259 | 0,3978864858 | |||
| 1,2 | 4,9712110049 | 0,4790843682 | 4,9942427541 | ||
| 1,25 | -0,0499582642 | 0,3975018913 | |||
| 1,3 | 4,9662151785 | 0,5188345574 | 4,9932436849 | ||
| 1,35 | -0,0539473856 | 0,3970851365 | |||
| 1,4 | 4,9608204399 | 0,558543071 | 4,992164841 | ||
| 1,45 | -0,0579347576 | 0,3966361948 | |||
| 1,5 | 4,9550269642 | 0,5982066905 | 4,9910062573 | ||
| 1,55 | -0,0619202472 | 0,3961550377 | |||
| 1,6 | 4,9488349394 | 0,6378221943 | 4,9897679715 | ||
| 1,65 | -0,0659037205 | 0,3956416345 | |||
| 1,7 | 4,9422445674 | 0,6773863577 | 4,988450024 | ||
| 1,75 | -0,069885043 | 0,3950959526 | |||
| 1,8 | 4,9352560631 | 0,716895953 | 4,9870524577 | ||
| 1,85 | -0,0738640791 | 0,3945179573 | |||
| 1,9 | 4,9278696552 | 0,7563477487 | 4,9855753184 | ||
| 1,95 | -0,0778406925 | 0,3939076119 | |||
| 2 | 4,9200855859 | 0,7957385099 | 4,9840186546 |
Majd ábrázoljuk grafikonon:
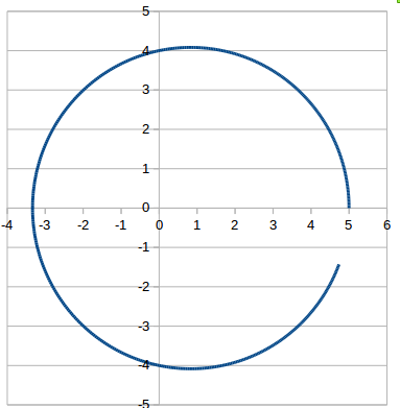
Az előző számolás eredményeként kapott pálya grafikonon, kb. 50 másodpercig kiszámolva. Jó látható, hogy szinte tökéletesen összejön az ellipszispálya.
Láthatjuk, hogy tökéletes ellipszis pálya lesz az eredmény.
De a mi a helyzet akkor, amikor kettőnél több test van, pl. egy egész bolygórendszer? Az alapszabály ilyenkor is ugyanaz: a köztük fellépő vonzerő távolság négyzetével fordítottan, tömegeik szorzatával egyenesen arányos lesz. Tegyük fel, hogy van egy rendszerünk, amelyben van sok test, a számukat jelöljük $n$-nel. Az első testnek a tömege legyen $m_1$, helye $\v{x_1}$, sebessége $\v{v_1}$, gyorsulása $\v{a_1}$, a rá ható erő vektora $\v{F_1}$. Vegyük észre, hogy itt vastagon van szedve a betű és az alsó index is. Most nem a vektor első eleméről van szó, hanem ez az „1-es vektor”. Hasonlóan a 2. testnek a tömege $m_2$, helye $\v{x_2}$, sebessége $\v{v_2}$, gyorsulása $\v{a_2}$, a rá ható erő vektora $\v{F_2}$. És így tovább, egészen az utolsó testig.
Na most akkor milyen erők hatnak az egyes testekre? Az 1-es testre hat a 2-es $G \frac{m_1 m_2}{|\v{x_2} - \v{x_1}|^2}$ erővel.
Ami új, hogy a nevezőben kivonunk két vektort, és a különbségnek a nagyságát vesszük. Mit jelent ez? Azt, hogy az egyik ponthoz képest merre és milyen messze van a másik. Pl. a merre van a vonalzón 10 cm-es vonás a 25 cm-es vonáshoz képest? Vonjuk ki a két számot: 10 - 25 = -15. Tehát 15 centivel visszább. És ugyanez az analógia működik a helyeket jelölő vektorokra is: Hogy merre van az $\v{x_2}$ az $\v{x_1}$-hez képest? Vonjuk ki egymásból a két vektort, és akkor meglátjuk, hogy egyik főirányban ennyire, a másikban annyira, a harmadikban amannyira. És mit jelent, hogyha ennek a különbségnek vesszük az abszolút értékét? A távolságot. Milyen messze van a vonalzón a 10 centis vonás a 25 centistől. Először vonjuk ki egymásból a két számot: 10 - 25 = -15. És vegyük az abszolút értékét: 15 centire. Ugyanígy kell eljárni a két hely esetében is. Két pont távolságát úgy írjuk le, hogy vesszük a helyüket leíró vektorok különbségét és annak vesszük az abszolút értékét. Ez a matematikai eszköz 2 pont távolságának a leírására.
Na, visszatérve a témához. Előbb leírtuk, hogy mekkora erővel hat a 2. test az 1.-re. Hat rá még a 3-as test is $G \frac{m_1 m_3}{|\v{x_3} - \v{x_1}|^2}$ erővel. Ugyan így hat rá a 4-es is (érdemes megfigyelni, hogy csak kicseréljük az alsó indexeket). És így tovább egészen az utolsó testig. Majd ezeket az erőket össze kell adni, hogy megkapjuk a tényleges erőt, amely szerint mozogni fog a test. Szóval akkor az 1. testre ható erő:
$$ \v{F_1} = \sum_{i=2}^n G \frac{m_1 m_i}{|\v{x_i} - \v{x_1}|^3}(\v{x_i} - \v{x_1}) $$
A 2. testre ható erőknél is ez a szabály. Hat rá az 1.-es és 3.-tól kezdve a többi. Önmagát nem vonzza, mert saját magától nulla távolságra van, és az nullával való osztás lenne. Így az összegből a 2-est ki kell hagyni, tehát az $i = 2$ eset nem játszik. Így a második testre ható erő:
$$ \v{F_2} = \sum_{i=1}^n G \frac{m_2 m_i}{|\v{x_i} - \v{x_2}|^3} (\v{x_i} - \v{x_2}); i \ne 2 $$
Hasonlítsuk össze a két egyenletet és nézzük, meg, hogy mi a különbség az 1-es és a 2-es testre ható erők esetében. Ha megtettük, akkor ezek alapján felírhatjuk az általános egyenletet tetszőleges $j$-edik testre:
$$ \v{F_j} = \sum_{i=1}^n G \frac{m_j m_i}{|\v{x_i} - \v{x_j}|^3} (\v{x_i} - \v{x_j}); i \ne j $$
És ez az a törvény, amely szerint a tetszőleges számú és tömegű test mozgása szimulálható.
Egy mini „naprendszer” szimulációja. A központi test 1000-szer nehezebb, mint a bolygók. A szimuláció képre kattintással indítható, illetve megállítható. A szimuláció nem tökéletes, ha két test nagyon közel kerül egymáshoz, akkor szimuláció hibája nagyon megnövekszik, ezért az ütköző testek tovaszállnak.
Ha elég kis lépésközzel számolunk, akkor akár a naprendszerünk bolygóinak mozgását is viszonylag pontosan lehet szimulálni. És még azt is, ahogy több bolygó egymásra hat. Így határozták meg annak idején a Neptunusz helyét. A többi bolygóra való gravitációs hatása alapján.
Amíg az első két test problémának létezik analitikus megoldása, addig az általános N-test problémának nincs analitikus megoldása. Azt mindig számítógéppel kell szimulálni. Számos dolog van a mindennapi életben, amit csak a teljes szimuláció segítségével lehet meghatározni. Ilyen pl. az időjárás előrejelzés szimulációja. Manapság már pontosan előre jelezhető, hogy egy hidegfront hány órakor éri el hazánkat, és azt is, hogy hogyan fog majd mozogni, és még azt is, hogy hol várható majd sok csapadék. És ezek a szimulációk is mind-mind azon az alapelveken működnek, amit ebben a részben tárgyaltunk meg.
