5. Valószínűség
Ahhoz, hogy ellenőrizzük, hogy a természetről alkotott elméletünk helyes-e, kísérleteznünk kell. Valamikor az elmélet egy egzakt kimenetet jelez előre. Ilyen pl. a ferde hajítás. Ezt viszonylag egyszerűen lehet mérni, és ellenőrizni. És vannak elméletetek, amelyek nem ilyen egzaktak. Például ilyen elmélet az, hogy „a jó dobókockán minden szám azonos 1/6 (kb. 16,7%) eséllyel jöhet ki”. Hogyan ellenőrizhetjük, hogy egy adott dobókocka elég jó-e? Hogyan ellenőrizhetjük, hogyha egy elmélet azt jelzi előre, hogy valaminek az esélye 1 az 5-höz, akkor az valóban annyi-e? Ebben a részben erről fogok írni.
A valószínűség
Mit jelent az, hogy esemény bekövetkezési valószínűsége például 50%? Azt, hogyha az adott kísérletet elvégezzük sokszor, akkor várhatóan az esetek 50%-ban fog megtörténni a várt esemény. Például, ha egy pénzt feldobunk, akkor annak az esélye, hogy fej legyen 50%. Ez azt jelenti, hogyha 20-szor dobjuk fel, akkor várhatóan 10-szer fog fej állásban landolni. Próbáljuk ki! Feldobtam egy pénzt 20-szer és 10-szer lett fej. Aztán megint hússzor, 4-szer lett. Harmadik próbálkozásra 11-szer lett. Negyedikre 9-szer. Ötödikre 8-szor. Ezek alapján elmondhatom-e, hogy tutira 50% eséllyel landol a pénzem fejen? És nem mondjuk 45%-kal? Egyelőre még nem.
A lehetetlen esemény valószínűsége 0. A biztosan megtörténő események valószínűsége 1 (azaz 100%). A valószínűség soha sem lehet 0-nál kisebb, vagy 1-nél nagyobb. Ha mégis ez jönne ki, akkor valamit elszámoltunk.
Várható érték
Vegyünk pl. egy dobókockát. Vannak rajta számok 1-től 6-ig. Ha a kocka igazságos, akkor minden szám azonos 1/6-os valószínűséggel (kb. 16,6%) jöhet ki. A várható érték a lehetőségek átlaga a valószínűséggel súlyozva. Azaz a kocka esetén: 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = 3,5. Tehát a kockadobás várható értéke 3,5. Vagy mondhatjuk úgy is, hogy átlagosan ennyit dobunk a kockával. Vagy pl. dobálózhatunk pénzzel. Ha fejet dobunk, akkor az érhet 1-et, ha írást, akkor az 0-t. Mind a kettő esélye 1/2. A várható érték 0,5.
A várható értékek összeadhatóak. Tehát, hogyha kétszer dobunk a kockával, és összeadjuk a pontokat, akkor várhatóan az összeg 7. Ha 100-szor dobunk a kockával, akkor várhatóan a 100 dobásban a pontok összege 350 lesz. Ha 1000-szer dobunk pénzzel és összeszámoljuk a fejeket, akkor várhatóan 500-at fogunk számolni.
Az előzőek alapján általánosítsunk! Legyen $p$ egy esemény bekövetkezésének a valószínűsége. Legyen $n$ a próbálkozások száma. Ekkor az $n$ próbálkozás után várhatóan $np$-szer fog bekövetkezni az esemény.
Ez azonban nem garancia arra, hogy pont ennyi is jön. Ez egy átlag.
Gyakorlatban a várható érték sok mérés után úgy becsülhető, hogy vesszük mért adatok átlagát.
Binomiális eloszlás
Annak az esélye, hogy egy kiegyensúlyozott pénzérmével fejet dobjunk 50%. 1 fejnek az esélye 50%. Annak az esélye, hogy ezután még egy fejet dobjunk az 50% 50%-a, tehát annak az esélye, hogy egymás után 2 fejet dobjunk 25%. Annak az esélye, hogy a 2 fej mellé dobjunk egy harmadikat 50%. Mivel már 2 fej esélye is csak 25%, ezért annak az 50%-a, azaz 12,5% lesz annak az esélye, hogy egymás után 3-szor dobjunk fejet. Látható a minta. Két egymástól független esemény együttes bekövetkezésének a valószínűsége az események valószínűségének a szorzata. Így hát annak az esélye, hogy 2 dobókockával 2 hatost dobunk 1/6*1/6 = 1/36 (kb. 2,78%). Annak az esélye, hogy pénzzel fejet, majd dobókockával hatost dobunk 1/6*1/2 = 1/12 (kb. 8,33%). És így tovább.
Annak az esélye, hogy kockával 1-est dobunk 1/6. Annak az esélye, hogy 4-est dobunk 1/6. Annak az esélye, hogy a 4-es és 1-es közül az egyiket dobjuk 1/6 + 1/6 = 2/6 = 1/3. Hogyha van kettő vagy több olyan eseményünk, amely kizárja egymást, akkor annak a valószínűsége, hogy az egyik bekövetkezik a kettő közül a külön-külön bekövetkezés esélyének az összege. De ez csak egymást kizáró események esetén működik így. Ha a több esemény egyszerre is megtörténhet, akkor nem lehet a valószínűségeket összeadni.
Mennyi lehet az esélye annak, hogy 10 pénzfeldobásból mondjuk 4-szer jön ki fej? Ha tízszer dobjuk fel a pénzt, és egy adott sorrendet várunk, akkor 10 esemény valószínűségét össze kell szorozni. Fej és írás egyaránt 1/2 valószínűséggel jön ki, így ezt 10-szer összeszorozva 1/1024-et kapunk, ami nagyon kicsi.
Viszont többféle sorrend is létezik, amelyben 10 dobásból 4-szer jön fej. És egyszerre csak egyféle sorrendben jöhetnek ki a dobások, tehát két különböző sorrend egymást kizárja. Így a több megfelelő sorrend valószínűsége összeadható.
Hány olyan sorrend létezik, amelyben 10 dobásból 4-szer jön fej? Két eset lehetséges. Az egyik helyzet az, hogy 9 dobás után van 3 fejünk, erre dobjuk 10.-nek a 4.-et. A másik helyzet pedig az, hogy 9 dobás után van 4 fejünk, erre pedig 10.-nek dobunk egy írást. Ha tudjuk, hogy 9 dobásból hányféle sorrendben dobhatunk 3 illetve 4 fejet, akkor a kettő összeadásával megkapjuk, hogy hányféleképpen lehet 10 dobásból 4 fejet kapni.
Aztán, hogy megkapjuk, hogy 9 dobásból hányféleképpen lehet 3 fej, akkor megint 2 esetet kell nézni: a 8 dobásból 2 fejre, dobtunk egy fejet, illetve a 8 dobásból 3 fej helyzetére dobtunk egy írást, a kettőt össze kell adni. És így tovább mindaddig, amíg el nem jutunk olyan egyszerű esetekhez, amelyeket már könnyen megadhatunk. Ilyen eset az, hogy csak egyféleképpen lehet az, hogy az összes dobásunk fej vagy az összes dobásunk írás. Szintén egyféleképpen lehet az, hogy egyszer sem dobtuk, és nyilván 1 fejet sem kaptunk.
Alább látható, az ún. Pascal-háromszög, amely az esetek számát segít megadni.
Pascal háromszög. Minden elem a tőle balra lévő és átlósan balra lent lévő elem összege. Megadja, hogy adott számú pénzfeldobásból hányféle sorrendben jöhet ki fej. (rákattintva nagyobban is látszik) (CC-BY)
A matematikában ezt a dolgot tehát, hogy valamennyi (N) dobásból hányféleképpen lehet valamennyi (K) fej, úgy nevezzük, hogy binomiális együttható. És így jelöljük: $N \choose K$, mondani pedig úgy szoktuk, hogy „N alatt a K”. Látható, hogy, ami nekünk kell az az $10 \choose 4$, ami 210. Egy adott sorrend esélye 1/1024. Annak az esélye pedig, hogy 10 dobásból 4-szer dobunk fejet ezek szerint 210/1024. Azaz kb. 20,5%.
Az általános esetben a számolt esemény valószínűsége nem 50%. Itt most speciálisan a fej és az írás valószínűsége is 50% volt. Nézzünk egy másik problémát. Dobókockával dobunk 12-szer. Mennyi az esélye, hogy pont 2-szer dobunk hatost?
Annak az esélye, hogy hatos 1/6. Annak az esélye, hogy nem hatos 5/6. Azaz egy olyan dobássorban, ahol pont 2 hatos van 2-szer kell szorozni az 1/6-ot. A maradék 10 esetben pedig az 5/6-ot. Tehát egy adott 2 hatost tartalmazó sorrendre az esély: (1/6)2(5/6)10. Valamint ${12 \choose 2} = 66$. A kettőt összeszorozva azt kapjuk, hogy kb. 29,6% az esélye a 2 hatosnak 12 dobásból.
Tehát az általános esetben, amikor valamilyen $N$-szer végzünk el egy kísérletet valamilyen $k$ darab találatot várunk, és egy találat esélye $p$. Akkor Annak az esélye, hogy N-ből k-szor van találat ennyi:
$$ {N \choose k} p^k (1-p)^{n-k} \label{eq:binomial_weight} $$
Ez ún. binomiális eloszlás súlyfüggvénye.
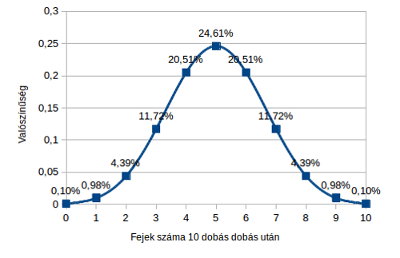
10 pénzdobás után a valószínűsége annak, hogy hány dobás lesz fej. Látható, hogy az 5 fejnek van a legnagyobb valószínűsége. (CC-BY)
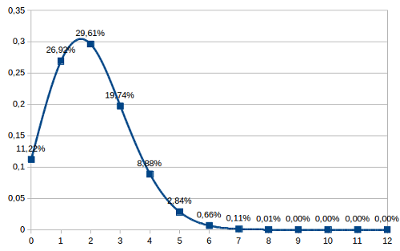
12 kockadobás után a hatosok számának a valószínűsége. Látható, hogy annak a legnagyobb a valószínűsége, hogy 2-szer jön hatos. Nagy számú hatos dobás esélye rendkívül pici - 12 hatosra már 250-szer kisebb az esély mint a lottóötösre. (CC-BY)
Szórás
Korábban említettük még a várható értéknél, hogy pl. ha 1000-szer dobjuk fel a pénzt, akkor várhatóan 500-szor esik fej állásban. Na most valóban 1000-szer dobjuk fel, valami 500 körüli szám lesz a fejek száma, de általában nem pont 500.
A szórás adja meg, hogy a mérés mennyire tér el az átlagtól. Ha kicsi a szórás, akkor kevésbé tér el. Ha nagy, akkor jobban.
A kiszámolásához kell egy kis matematika. Legyen $X$ egy véletlenszerűen mért érték, mondjuk kockadobás. Jelöljük hegyes zárójellel a várható értékét: $\left< X \right>$. Ekkor a szórás négyzetének képlete ez: $\left< \left( \left< X \right> - X \right)^2 \right>$. Vagy más formája is ismert: $\left< X^2\right> - \left< X \right>^2$ (négyzetek átlaga mínusz az átlagok négyzete). Ennek a gyöke a szórás.
Például feldobunk egy pénzt százszor.
Majd ezt a százas sorozatot 10-szer ismételjük.
A 10 százasban a következő mennyiségben jött fej: 47, 43, 48, 55, 50, 57, 48, 46, 48, 40.
Az átlag: 48,2.
Na most vesszük az egyes adatok különbségét az átlagtól és négyzetre emeljük őket:
(47 - 48,2)2 = 1,44
(43 - 48,2)2 = 27,04
(48 - 48,2)2 = 0,04
(55 - 48,2)2 = 46,24
(50 - 48,2)2 = 3,24
(57 - 48,2)2 = 77,44
(48 - 48,2)2 = 0,04
(46 - 48,2)2 = 4,84
(48 - 48,2)2 = 0,04
(40 - 48,2)2 = 67,24
Ezeknek az átlaga 22,76.
Ez az ún. szórásnégyzet.
A gyöke pedig 4,77; a szórás.
Tehát ennek az adatsornak a szórása kb. 4,77.
Az elvont fogalmat, mint pl. egy kockadobás értéke úgy nevezzük, hogy valószínűségi változó. Valószínűségi változó lehet egy kockadobás értéke, vagy 1000 pénzfeldobásból a fejek száma. Tehát egy olyan szám, amely véletlenszerűen jön ki.
Dobókockán minden szám azonos eséllyel jöhet ki. Az ilyenre azt mondjuk, hogy egyenletes eloszlású. Az adott számú pénzfeldobásból a fejek száma nem egyenletes, mert rendkívül esélytelen, hogy 1000 feldobásból mindegyik fej vagy mindegyik írás legyen. Viszont elég jó eséllyel kapunk 500 körüli darab fejet. Több ismételt próbálkozás után a sikeres próbálkozások száma binomiális eloszlású, ahogy az előző részben láttuk. Ezen fogalmak bevezetése azért jó, mert kevés szóval lehet sokat mondani. Ha azt mondom, hogy egy binomiális eloszlású valószínűségi változó, akkor olyan dologra tessék gondolni, mint a sokszor feldobott pénz esetén a fejek száma. Ha azt mondom, hogy egyenletes eloszlású valószínűségi változó, akkor meg olyanra kell gondolni, mint egy dobókocka, amelyben minden szám azonos eséllyel jöhet ki. És nem kell egy bekezdést írnom róla mindig.
Szintén érdemes most elmagyarázni, hogy mit jelent azt, hogy két valószínűségi változó független. Ez azt jelenti, hogy az egyik kimenetét nem befolyásolja a másik eredménye. Egy pénzfeldobás eredménye nem fogja befolyásolni a következő pénzfeldobás eredményét. Így a két dobás független. Viszont ha egy átlátszó műanyag lapra rögzítjük a két pénzérmét, így úgy dobunk velük, akkor azonos állásban landolnak, és így már függenek egymástól.
Na most akkor legyen egy binomiális eloszlású valószínűségi változónk. $n$-szer próbálkozunk, és egy adott próba esetén a siker esélye legyen $p$. A valószínűségi változó a sikeres próbák száma. Ennek a változónak a szórása várhatóan ennyi: $\sqrt{n p (1-p)}$. Tehát ha 100-szor dobunk fel egy pénzt, a fej esélye 50%, azaz 0,5. A fenti képletbe behelyettesítve 5-öt kapunk. A korábban mért 10-szer 100 dobás fejeinek a szórása egyébként nagyjából ott is van, majdnem 5 jött ki.
Ha úgy általában egy valószínűségi változó szórására vagyunk kíváncsiak pontos mérések nélkül, akkor az a következőképpen tehetjük meg.
Vegyük egyes értékek eltérését az átlagtól, és emeljük ezt az eltérést négyzetre.
Majd ezeket az értékeket átlagoljuk súlyozottan az adott érték előfordulásának megfelelően, hogy megkapjuk a szórásnégyzetet.
Példa dobókocka dobás esetén tudjuk, hogy az átlag 3,5.
Az egyes dobások négyzetes eltérése az átlagtól:
(1 - 3,5)2 = 6,25
(2 - 3,5)2 = 2,25
(3 - 3,5)2 = 0,25
(4 - 3,5)2 = 0,25
(5 - 3,5)2 = 2,25
(6 - 3,5)2 = 6,25
Mivel minden dobás valószínűsége 1/6. Ezekkel beszorozva a kapott számokat és összeadva a szórásnégyzet 35/12 azaz kb. 2,917 lesz. A gyöke pedig egy 1,708 körüli szám.
A szórásnégyzetek összeadódnak. Tehát ha van két független valószínűségi változónk, az egyiknek 3 a szórása, a másiknak meg 4, akkor a szórásnégyzeteik összege 9+16 = 25. Tehát a szórás az összegüknek 5 lesz.
Poisson eloszlás
Tegyük fel, hogy van egy radioaktív mintánk (mondjuk urán, hogy ne kapjunk sugárfertőzést). Mellé rakunk egy Geiger-számlálót. 24 óráig számoljuk a részecskéket, majd azt kapjuk, hogy 864078 részecskét számoltunk. Egy napban 86400 másodperc van, tehát átlagosan másodpercenként kb. 10 részecskét fogunk.
Ilyenkor felmerülhet a kérdés, hogy mennyi a valószínűsége annak, hogy 1 másodpercben pontosan 10 részecskét fogunk? És annak, hogy 9-et, esetleg egyet sem, netán 100-at? Amikor dobókockát vagy pénzt dobáltunk, akkor fix volt a próbák száma, és ismert volt a keresett esemény bekövetkezési valószínűsége. Ekkor simán csak össze kellett szorozni a próbák számát a valószínűséggel és megkaptunk, hogy átlagosan hányszor jön be a várt esemény. Alapjában véve nincs ez máshogy itt sem. A bomlás megtörténhet bármelyik pillanatban az 1 mp alatt. Nem tudjuk, hogy pontosan hány pillanat van 1 másodpercben, de azért jelöljük el $n$-nel. Annak meg az esélye, hogy egy adott pillanatban bekövetkezik a bomlás legyen a valószínűsége valamilyen $p$. Tudjuk, hogy a példánkban $np = 10$. Azaz 1 másodperc alatt 10 bomlást várunk. 1 másodpercben nagyon-nagyon sok pillanat van, tehát az $n$ hatalmas szám. 1 pillanat nagyon rövid, annak az esélye meg, hogy pont egy adott pillanatban történjen egy bomlás nagyon-nagyon kicsi. Tehát $p$ majdnem nulla. A nagyon nagy számot összeszorozva a nagyon kicsivel kapunk egy emberi léptékkel felfogható számot. Ezt a hatalmas $n$-t és pirinyó $p$-t csak be kell helyettesíteni a binomiális eloszlás képletébe ($\eqref{eq:binomial_weight}$), illetve a $k$ helyére a keresett másodpercenként eseményszámot. Ezt kiszámoljuk és meg is van, hogy mennyi a valószínűsége annak, hogy pont $k$-szor kattan a Geiger-számláló 1 másodpercben.
Nyilván macera ezt így kiszámolni közvetlenül. Viszont analízis segítségével megadható a képlet, amit használnunk kell. Legyen $\lambda$ a várható érték, esetünkben 10, $k$ pedig a szám, ahány másodpercenként eseménynek a valószínűségét keressük. Ekkor a képlet, amit használnunk kell:
$$ \frac{\lambda^k e^{-\lambda}}{k!} $$
A ! a faktoriálist jelenti tehát $n! = 1*2*3*...*n$. Az $e$ pedig a természetes alap (2,71828...).
Na most akkor mennyi az esélye, hogy a másodpercenként átlagosan 10 kattanást adó radioaktív forrás, pont 10-et kattint egy másodpercben? Ha behelyettesítünk, és számológéppel kiszámoljuk azt kapjuk, hogy kb. 12,5% eséllyel. 11 találatra 11,3% az esély. 12-re 9,48%. 20-ra 0,187%, tehát óránként kb. 6-szor megszalad annyira, hogy a vártnak a dupláját adja 1 másodpercben. 5 találatra 3,78%. 2 találatra 0,226%, ezt azt jelenti, hogy óránként kb. 10-szer van olyan másodperc, amikor csak 2 kattanás történik.
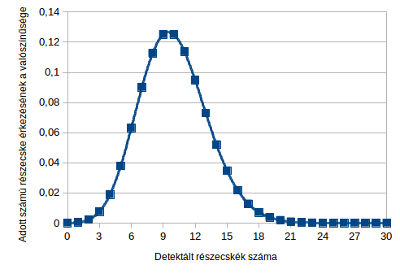
Annak a valószínűsége, hogy 1 másodperc alatt az adott számú részecske érkezik a detektorba. Látható, hogy a legnagyobb esélye annak van hogy 10 körüli számban érkeznek a részecskék. (CC-BY)
A radioaktív bomlás egy jó példája az ún. Poisson-eloszlású valószínűségi változónak. Ugyanis rendelkezik a következő tulajdonságokkal:
- A mérés ideje alatt gyakorlatilag állandó a sugárzás erőssége.
- Egész számú részecske érkezik a forrásból (nincs fél meg negyed kattanás)
- Az egyik részecske kibocsátása nem befolyásolja, hogy a következő mikor következik (azaz a részecskék egymástól függetlenül jönnek).
- Két kattanás nem történhet azonos időpillanatban (bár nagyon-nagyon ritkán beállíthat 2 részecske egyszerre a detektorba, de ez az ilyen esetek elhanyagolhatók.
- A mérés hossza nem befolyásolja a kibocsátás mértékét.
- Csak arról beszélhetünk, hogy hány esemény történt meg, arról nem, hogy hány esemény nem történt meg.
A Poisson eloszlás nem csak radioaktív bomlás esetén használatos. Hanem alkalmazható bármire, amely megfelel a fenti listának. Pl. tegyük fel, hogy az országunkban átlagosan 100 évente történik egy nagy földrengés. Mennyi az esélye, hogy a következő 100 évben 2 nagy földrengés történik? A képlet alapján a válasz kb. 18,3%. 3 nagy földrengésre kb. 6,1%, és így tovább.
Ennek az eloszlásnak a szépsége, hogy csupán az átlag ismeretében megmondható, hogy az adott időszakban milyen valószínűséggel várható adott számú esemény, függetlenül az időszak hosszától. Tehát a radioaktív bomlásunkra visszatérve. A mintánk átlagosan tizedmásodpercenként bocsát ki egy részecskét. Mennyi a valószínűsége, hogy egy tizedmásodperces időszakban 2-t bocsásson ki? 18,3%. Hogy hármat? 6,1%. Pontosan ugyanúgy, mint a földrengések esetén.
Poisson eloszlás szórásnégyzete megegyezik az átlaggal. Tehát a szórása az átlag gyöke. Tehát, ha van egy Poisson-eloszlású valószínűségi változónk mondjuk 100-as átlaggal, akkor annak a szórása 10 lesz.
Ha két Poisson-eloszlású valószínűségi változót összeadunk, az eredmény szintén Poisson-eloszlású lesz, melynek az átlaga a kettő átlagának az összege. Tehát ha 1 másodperc alatt átlagosan 10 kattanás jön, akkor 2 másodperc alatt átlagosan 20 fog jönni. Az 1 másodperc alatti kattanások száma, és a rákövetkező másodpercben lévő kattanások száma egyaránt Poisson-eloszlású és 10 átlagú. A 2 másodperc alatti 20 kattanás átlagú valószínűségi változó szintén Poisson-eloszlású lesz csak 20-as átlaggal.
Folytonos eloszlások
Egy dobókockán hatféle szám van, és dobáskor ezen számok egyike lesz az eredmény. Az eddigi eloszlásainkban konkrét kimenetekről volt szó, és mindegyik kimenetnek meghatározott valószínűsége volt. Ezek voltak ún. diszkrét eloszlások. De vannak olyan esetek is, amikor végtelen sok kimenet lehetséges. Ilyen például a célba dobás. A céltáblát bárhol eltalálhatod. Végtelen sok helyen találhatod el. Itt nincs értelme arról beszélni, hogy mennyi az esélye annak, hogy a táblát pont egy adott pontban találod-e el. Mert az egy pontban való találat esélye gyakorlatilag 0. Viszont arról már van értelme beszélni, hogy mekkora eséllyel találunk el egy területet a céltáblán, mondjuk a közepén lévő kis kört. A pontok a céltáblán közel vannak egymáshoz, egy folytonos területet alkotnak, amelyen belül bármelyik pont eltalálható. Azoknak a valószínűségi változóknak az eloszlásánál a csoportját, amelyek ezzel a tulajdonsággal rendelkeznek, úgy nevezzük, hogy folytonos eloszlások.
A diszkrét eloszlásoknál minden lehetőséghez tartozik egy konkrét valószínűség a valószínűségi súly. Ha összeadjuk az összes lehetőséghez tartozó valószínűséget, akkor 1-et kapunk, mert tuti, hogy valamelyik lehetőség bekövetkezik. A folytonos eloszlásnál kicsit más a helyzet. Ott minden egyes pont eltalálásának a valószínűsége gyakorlatilag nulla, olyan kicsi. Így ott kicsit máshogy kell a pontokhoz állni, hogyha valószínűségről beszélünk. Azt kell csinálni, hogy fogni kell egy piciny területet az adott pont körül; majd megadni, hogy mekkora valószínűséggel találhatunk abba a piaci területbe. Ezután a valószínűséget és a területet el kell osztani egymással. A kapott szám lesz az ún. valószínűségi sűrűség. Minden ponthoz hozzárendelhető egy ilyen sűrűség, ez az ún. valószínűségi sűrűség függvény. A lehetetlen értékeknél a sűrűség 0, a lehetségeseknél ennél több. Minél valószínűbb, hogy egy adott pont körül szóródik a találat annál nagyobb ott a sűrűség.
A sűrűségnek nincs felső korlátja, azonban a sűrűségfüggvény görbéje alatti terület nagysága mindig 1.
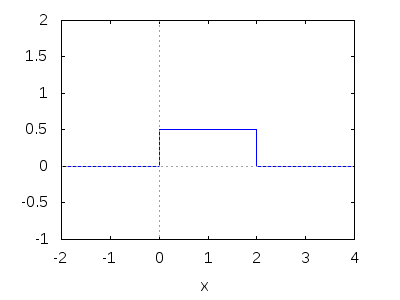
Folytonos egyenletes eloszlás. Itt 0 és 2 közötti véletlen számokról van szó. Látható, hogy a tartományon kívül a sűrűség 0, mert ott nem lehetségesek értékek. Míg a tartományon belül mindenhol azonos a sűrűség: minden szám azonos eséllyel jöhet ki. (CC-BY)
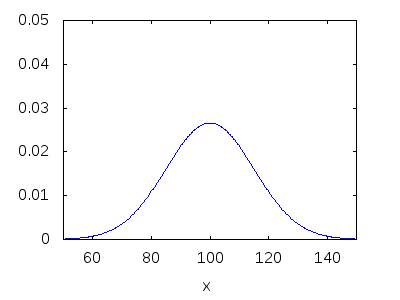
Normál eloszlás, 100-as várható értékkel, 15-ös szórással. Látható, hogy a legtöbb találat a 100-as körül szóródik, másfelé kisebb eséllyel kapunk találatot. (CC-BY)
Normál eloszlás
Tegyük fel, hogy van egy valószínűségi változónk, amelynek ismert az eloszlása, várható értéke és a szórása. Vegyünk nagyon sokszor (legalább 1000-szer) mintát belőle, tehát dobunk a pénzérmével vagy kockával, vagy akármivel, sokszor, és adjuk össze a számokat. Ekkor az összeg egy olyan valószínűségi változó lesz, amely jó közelítéssel ún. normál eloszlású lesz. 1Ez a központi határeloszlás tétele miatt van. És ez független attól, hogy a kiinduláshoz használt valószínűségi változó milyen eloszlású. Csupán össze kell adni a várható értékeket és a szórásnégyzeteket, és megkapjuk a normál eloszlás paramétereit. Ez az eloszlás azért fontos, mert a gyakorlatban, amikor méréséket vagy statisztikát készítünk általában nagy mennyiségű mintával dolgozunk: több ezer mérést végzünk, azonos körülmények között. Mivel a mérést azonos körülmények között végezzük, a várható érték és a szórás is azonosnak tekinthető. Miközben a mérési eredményeket átlagoljuk össze is adjuk őket, ezért elmondható, hogy a kapott eloszlás gyakorlatilag normál lesz.
Nézzünk egy példát. Pénzfeldobás. Fej vagy írás. A fej jelentsen 1-et az írás 0-át. 50-50% eséllyel jöhetnek ki. Sok dobás után a dobások átlaga 0,5 tehát a várható értéke ennyi. A pénzfeldobások szórásnégyzete 0,25. Ha a pénzfeldobásokat összeadjuk, akkor az átlag és a szórásnégyzet is összeadódik. Tehát 10000 dobás után az átlag 5000, a szórásnégyzet 2500 lesz. Szigorúan véve a kapott valószínűségi változó eloszlása binomiális, viszont ekkora minta esetén az eloszlás már nagyon jól közelíti a normál eloszlást.
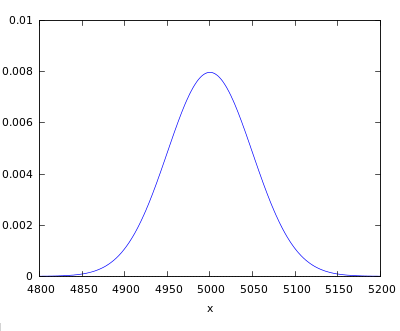
10000 pénzdobásból a fejek száma. Ilyen nagy számú dobás esetén már jól közelíthető az eredmény normál eloszlással. (CC-BY)
Ugyanez igaz a Poisson-eloszlásra is. Ha van egy Poisson-eloszlású valószínűségi változónk, 10000-es átlaggal és 10000-es szórásnégyzettel, akkor az is nagyon jól közelíti a normál eloszlású változót hasonló paraméterekkel.
A Normál eloszlás sűrűségfüggvényének a képlete ez:
$$ f(x) = \frac{1}{\sqrt{2 \sigma^2 \pi}} e^{-\frac{(x - \mu)^2}{2 \sigma^2}} $$
A képletben az $e$ a természetes alap, a $\pi$ a szokásos 3,1415..., a $\sigma$ a szórás, a $\mu$ pedig az átlag. Szúrj be bármilyen számot, és megkapod az adott eloszláshoz tartozó haranggörbét.
Normál eloszlás esetén a találatok 68%-a 1 szóráson belül van. 95%-a már 2 szóráson belül. 99,7%-uk pedig 3 szóráson belül van. Ez a 68-95-99,7 szabály egy könnyen megjegyezhető szabály arra, hogy egy mérés után mekkora eltérés várható az átlagtól, illetve, hogy a mért eredmény valóban normál eloszlású-e.
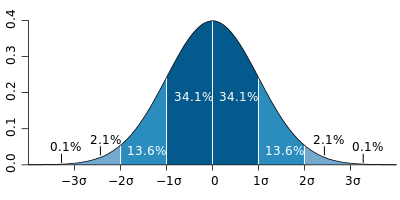
68-95-99,7 szabály. Normál eloszlás esetén a találatok 68%-a 1 szóráson, 95%-a 2 szóráson, 99,7%-a pedig 3 szóráson belül fog esni. (Forrás szerző CC-BY)
A fentiek alapján már tesztelhető egy pénzérme arra, hogy valóban 50-50% eséllyel dob fejet. Ha egy hibátlan pénzérmével dobunk 10000-szer, akkor a várhatóan 5000-szer lesz fej, a szórásnégyzet pedig 2500 lesz (a binomiális eloszlás képlete alapján). Ennyi dobás után már jó eséllyel mondhatjuk, hogy a fejek számának az eloszlása normál. 2500 szórásnégyzethez a szórás 50. Tehát 68% eséllyel kapott fejek száma valahol 4950 és 5050 között lesz. 95% eséllyel a kapott fejek száma 4900 és 5100 között lesz. 99,7% esélye a kapott fejek száma 4850 és 5150 között lesz. Szóval ha feldobunk egy pénzérmét 10000-szer és 5200-szor lesz fej, akkor 99,7%-nál is több eséllyel tuti, hogy a pénzérme nagyobb valószínűséggel ad fejet, mint írást.
Eloszlások a fizikában
Vegyünk például egy gázt. Benne a részecskék egyenes vonalban mozognak, amíg bele nem ütköznek egymásba vagy az edény falába. Mekkora sebességgel mozognak a részecskék? Nyilván egyesével lemodellezni az összes részecskét egyszerre nagyon nehéz lenne. Ehelyett inkább megadják, hogy mekkora valószínűséggel mehet egy adott része egy adott sebességgel. Mivel végtelen sokféle sebességgel mehetnek, ez egy folytonos eloszlás lesz. Az ún. Maxwell-Boltzmann eloszlás.
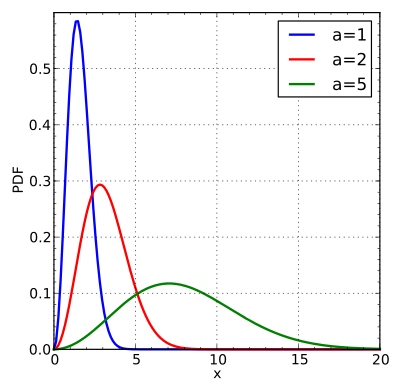
Maxwell-Boltzmann eloszlás különféle paraméterekre. Ez nem egészen haranggörbe, ugyanis aszimmetrikus. Nullától indul, és jobbra egy elnyúló farka van. Az $a$ paramétere a hőmérsékletnek felel meg. (forrás)
A másik hely, ahol a valószínűségek előkerülnek a kvantummechanika. Egy részecske sebessége és pozíciója egyszerre nem lehet pontosan ismert. Nem azért, mert a mérőműszereink rosszak, hanem mert alapból sem lehet így. A részecskéket csak valószínűségi alapon lehet leírni. Ez a Heisenberg-féle határozatlansági elv. A részecske lendületét és helyét egyaránt egy valószínűségi eloszlással lehet megadni. A két eloszlás szórásának a szorzata pedig nem lehet egy adott értéknél kisebb.
Amikor a fény részecskéje a foton egy ablaküveghez érkezik, akkor vagy átmegy rajta, vagy visszaverődik. Annak a valószínűségét, hogy átmegy-e egy diszktét valószínűségi eloszlással lehet megadni.
Az atomok körül sem keringenek az elektronok, hanem a pozíciójuk eléggé bizonytalan ahhoz, hogy egy atom méretű gömbben bárhol lehessenek. Az elektron helyét is egy valószínűségi sűrűségfüggvénnyel lehet megadni, pontosan.
Annak idején Einstein is mondott valami olyasmit, hogy „Isten nem kockajátékos”. Neki sem tetszett az ötlet, hogy véletlenszerűen történnek a dolgok az atomok szintjén. De azóta ez a véletlenség az a tudományos élet része lett. Ma már inkább azzal foglalkoznak a részecskék ezen tulajdonságát hogyan lehetne kihasználni. Ugyanis ezen tulajdonságaik lehetővé teszik a kvantumszámítógépek építését, amelyek számos problémát jóval gyorsabban képesek megoldani, mint a hagyományos számítógépek.
