3. Energia
Mi is az energia
Ebben a részben már elkezdünk egy kicsit belefolyni részletesebben a fizikába. Az első legfontosabb törvény, amit az ember megtanul fizikából az energiamegmaradás törvénye. Tehát van valamilyen dolog, ami megmarad, és nem vész el. De tulajdonképpen mi is az energia akkor?
Szerintem jobban nem lehetne ezt mondani, mint ahogy Feynman tette a saját előadásában: Tegyük fel, hogy van egy kisgyerekünk Dénes, akinek van egy fakocka szettje. 30 darab fakockája van, és ezekkel szeret játszani. Az apukája rendszeresen megszámolja a kockákat, és mindig 30 van. Aztán egyszer csak 28-at talál, aztán némi keresés után megtalálja a maradék 2-t az ágy alatt. Egy másik napon 29-et talál, aztán némi keresés után megtalál 1-et az udvaron, nyilván mert a kis komisz Dénes kidobta azt az ablakon. Egy másik napon már 32-t talál a szobában. Nem sokkal ezután kiderült, hogy átjött Béla és hozta ő is a fakockáit és itt hagyott kettőt. Az apukája ezt a 2 fakockát visszaadja Bélának. Telnek múlnak a napok, aztán egy napon, ismét 27 kocka van szanaszét szórva, 3-nak híja van, és nem találja az apuka sehol. Aztán eszébe jut, hogy talán a gyerek játékdobozában van. Viszont a Dénes nem szeretné, hogy elvegyék a játékát, ezért nem engedi az apukát, hogy kinyissa azt. Ezért az apuka kitalál egy rendszert. Tudja, hogy minden fakocka 10 dekás, tehát 0,1 kg tömegű. Ezért nem nyitja ki a gyerek játékdobozát, hanem rárakja egy mérlegre, és a következő megállapítást teszi:
$$ N + \frac{m_d}{0{,}1\mathrm{\,kg}} = \mathrm{állandó} $$
Ahol $N$ a földön heverő fakockák száma, $m_d$ pedig a játékdoboz tömege. Ha a kis Dénes berakott a játékdobozba egy kockát, akkor 1-gyel kevesebb lesz szét szórva, viszont a játékdoboz tömege pont egy kockával nagyobb lett. Így akárhány fakockát is tesz át a játékdobozba ez a képlet állandó lesz. Ez a képlet állandó lesz pár napig, aztán ismét azt látjuk, hogy kevesebb a kapott szám valamiért. Aztán meglátjuk, hogy az akvárium vize megemelkedett, mert a kis Dénes beledobálta a kockákat. Megmérhetjük, hogyha 1 kockát beledobunk, akkor 1 centivel (0,01 méterrel) növekszik a vízszint. Így a képletet kibővíthetjük az akvárium vízszintjének az emelkedésével, akkor ismét egy olyan képletet kapunk, amelynek az értéke állandó lesz:
$$ N + \frac{m_d}{0{,}1\mathrm{\,kg}} + \frac{h_v}{0{,}01\mathrm{\,m}}= \mathrm{állandó} $$
Ahol $h_v$ az akvárium vízszintje. Most már akár a játékdobozba, akár az akváriumba dobálják a kockákat, egy olyan képletünk van, amelynek az értéke állandó marad. Természetesen ez csak akkor igaz, hogyha közben nem dobálunk ki kockákat az ablakon, illetve Bélát sem engedjük be, hogy kockákat hagyjon itt nálunk. Vegyük észre, hogy eddig direktben számoltuk a kockákat, most már ezzel a képlettel indirekt következtethetjük ki, hogy mennyi kocka van. Tehát a játékdoboz tömegének változása, illetve az akvárium vízszintjének a változása alapján ki lehet következtetni, hogy mennyi kockánk van.
Látható, hogy a direkt kockaszámolásból eljutunk az indirekt kockaszámolásig. És az energia is pont így működik. Az energia nem egy fizikailag létező és mérhető dolog. Hanem egy olyan dolog, amelyet indirekt módon a dolgok helyzetéből, hőmérsékletéből, stb. ki lehet következtetni. És az energiát mindig úgy definiáljuk, hogy bármi is történjen az energiák összege állandó legyen.
Munka
Vegyük észre, hogy a fenti képletekben csaltam egy picit. Akár a doboz súlyáról, akár az akvárium vízszintjéről is van szó. Nem vontam ki azt a vízszintet illetve tömeget, ami a kocka nélküli akváriumhoz és játékdobozhoz tartozik. Ezt azért tehettem meg, mert az energia nem egy abszolút dolog. A mennyisége attól függ, hogy hogyan definiáljuk, viszont onnantól kezdve ez a mennyiség állandó. A fizikai folyamatok szempontjából nem az a fontos, hogy pontosan mennyi az energia, hanem az, hogy egy folyamat során hova megy. Mert ahhoz, hogy történjen valami, ahhoz az energiának mennie kell valahová. Na most ezt a dolgot, amikor az energia megy valahová úgy nevezzük, hogy munka. Ahhoz, hogy fizikai értelemben munkát végezzünk, energia kell. Ezért szokták a két adott energiát úgy is nevezni, hogy az adott dolog munkavégző képessége.
Amikor munka történik, akkor az energia átalakul egyik formájából a másikká. Aki a munkát végzi, annak az energiája csökken, amin a munkát végzi, annak az energiája pedig nő. Az energia és a munka mértékegysége a joule (J). A következőkben megnézzük, hogy milyen fajta energiákról is van szó.
Az energiák fajtái
Helyzeti energia
Minél magasabban van valami egy erőtérben, annál nagyobb a helyzeti energiája. A hétköznapokban egyetlen erőtérnek vagyunk erősen kitéve, ez a gravitációs erőtér. Ez az erő mindent lefelé húz. Ha valamit ez erő ellenében szeretnénk mozgatni, akkor munkát kell végeznünk. Ez a munka test tömegével egyenesen arányos. Tehát kétszer, háromszor nehezebb test emeléséhez kétszer, háromszor több munkát kell végezni. Egyenesen arányos még az emelés mértékével. Tehát kétszer, háromszor nagyobb mértékű emeléshez kétszer, háromszor több munkát kell végezni. Így a képlet az emelési munkára:
$$ W = mgh $$
Ahol a $W$ a munka mennyisége, $m$ a test tömege kilóban, $h$ az emelés mértéke méterben, $g$ pedig a súlyegyüttható, ami a Földön a felszínhez közel 9,81 newton/kilogramm. Ha ezeket összeszorozzuk, megkapjuk joule-ban, hogy mennyi munkát kellett végeznünk az emeléshez.
Az emelés során a testünkben tárolt kémiai energia alakult át helyzeti energiává, amelyet az emelt test kapott meg. Így a helyzeti energia képlete is $E = mgh$. Ahol $E$ az energia, $m$ a tömeg és $h$ a magasság, ahol a test van. Helyzeti energiánál a nulla szint és ezzel az energia nullpontja is szabadon választható.
Ha valamit felemelünk akkor energiát nyer, ha viszont leeresztjük vagy leejtjük, akkor a tárgy munkát végez és a helyzeti energiája alakul át valami más formára. Mivel ebben az irományban még csak a helyzeti energiát ismerjük, ezért nézzünk meg egy olyan esetet, amikor ezt a helyzeti energiát átadjuk egy másik testnek.
Tegyük fel, hogy van egy 1 tonnás (1000 kg-os) autónk, amelyet szerelni kell és ehhez fel kell emelnünk mondjuk 1 méterre. A fenti képlet alapján ahhoz, hogy ezt megtegyük kb. 10000 J helyzeti energiát kell adni neki.
Ezt megtehetjük úgy, hogy építünk egy ellensúlyos emelőgépet. Tehát egy csigán átvetett kötélen ellensúllyal felemeljük a kocsit. Na most az ilyen egyszerű csigás emelő olyan, hogy 1 méter emeléséhez 1 métert kell húzni kötélen. Ha elkezdjük pakolni az ellensúlyt azt látjuk, hogy az autó addig meg sem mozdul, amíg annyi súlyt rá nem tettünk az ellensúly oldalára, amelynek a leeresztése elegendő energiát biztosít az autó felemeléséhez. Tehát 1000 kg-ot kell pakolni ellensúly gyanánt, ha azt 1 méterrel leeresztjük, akkor pont 10000 J helyzeti energiát fogunk felhasználni, hogy felemeljük az autót 1 méterrel. Ez esetben csak egyszerűen áthelyeztük a helyzeti energiát az ellensúlyról az autóra, az energia megmaradt.
A jobboldali kosárba legalább 1 tonnát kell tenni, hogy a jobb oldal leeresztése közben végzett munka elegendő legyen a bal oldal felemeléséhez.
Azonban kevesebb tömeggel is lehetséges az emelés. Ugyancsak 10 kJ energiát szabadíthatunk fel úgy, hogy 250 kg-ot eresztünk le 4 méterrel. Ehhez csak az kell, hogy olyan szerkezetet építsünk, amelyben 1 méter emeléshez 4 méter kötelet kell húzni. Ez megvalósítható például egy csigasorral.
A jobboldalon 4 métert kell húzni, hogy a baloldal 1 méterrel emelkedjen, így az 1 tonnás tárgy felemeléséhez a jobboldalon 250 kg is elég lesz, azonban azt 4 méteren kell leereszteni.
A fenti példákban a helyzeti energia használatával emeltük meg az autót. Viszont egyáltalán nem szükséges, hogy ezt a helyzeti energiát ellensúllyal adjuk át. Az autókat általában fogaskerekes vagy menetes emelővel szoktuk felemelni. És aki már használt ilyet, az tudja, hogy egy ember 1 kézzel is képes jó sok tekerés után megemelni az autót. Tételezzük fel, hogy van egy ilyen karos emelőszerkezetünk, amelynek a karjának a hossza 16 cm. Egy fordulat a karral 1 milliméterrel megemeli az autót. Ez azt jelenti, hogy 1000 fordulat után megemeltük az autót 1 méterrel. Hogy lehetséges, hogy ilyen könnyen megemeltük az autót így? Képzeljük el, hogy a kart nem kézzel forgatjuk, hanem csigák segítségével átvezetjük egy ellensúlyra. Egy 16 centi sugarú kör kerülete kb. 1 méter. 1000 fordulathoz az 1 km kötél kell. Így az ellensúlynak 1000 métert kéne ereszkednie, hogy felemelje az autót. A szükséges 10 kJ energiát pedig ilyen magasról ereszkedés során már egy 1 kg-os test is megadja. Így az erő, amely a menetes emelő tekeréséhez kell egy 1 kg tömegű test súlyának felel meg. Vagy ha ezt beszorozzuk a $g$-vel akkor ez kb. 10 N (newton) erő. És egyáltalán nem szükséges, hogy az az ellensúly valóban ott legyen, kézzel is kifejthetjük ez a 10 N erőt. Ekkora erőt egy kisgyerek is kényelmesen kifejt.
Menetes emelővel hosszú úton de kis erővel emelhetünk nehéz tárgyakat.
Nézzük meg, hogy mit csináltunk előbb. 10000 J-nyi munkát fejtettünk ki 1000 m méter úton. A kettőt elosztva megkaptuk, hogy mekkora erőt kellett kifejtenünk: 10 N-t. Ez vezet el egy fontos képlethez, talán ahhoz, amit fizika órán az ember elsőként tanul meg:
$$ W = F \cdot s $$
Azaz a munka ($W$) az erő ($F$) és az erő irányában tett elmozdulás ($s$) szorzata. A munkát joule-ban, az erőt newtonban, az elmozdulást pedig méterben kell mérni.
A munka és energia, valamint az energiamegmaradás törvénye más jóval bonyolultabb feladatok megoldásában is segíthet. Például egy 100 kg-os tárgyat helyeztük egy 2 pilléres hídra. (a híd tömegét most a könnyítésként vegyük nullának). A tárgy a bal pillértől 20 centire, a jobbtól 80 centire van. Mekkora súly nehezedik az egyes pillérekre?
Képzeljük el, hogy a hidat megemeljük a bal pillérnél egy picit, egy nagyon pici $\epsilon$-nyit. Ekkor ott $F_A \epsilon$ munkát végzünk. Eközben a 100 kg-os tárgy $\frac{4\epsilon}{5}$-tel emelkedik fel. A jobb pillérnél pedig nem történik változás. Tehát $1000\mathrm{\,N} \frac{4\epsilon}{5}$ helyzeti energiát kapott. Az energiamegmaradás miatt a végzett munka egyenlő azzal az energiával, amennyit a tárgy helyzeti energiaként kapott. Így az egyenlet: $F_A \epsilon = 1000\mathrm{\,N} \frac{4\epsilon}{5}$. Ha kiosztjuk az $\epsilon$-t meg is vagyunk, hogy baloldali pilléren $F_A=$ 800 N erőt kell kifejtenünk. Hasonlóan alkalmazhatjuk ugyanezt a módszert a jobb pillérre. Megemeljük egy picivel, így ott $F_B \epsilon$ munkát végzünk. A baloldali pillérnél nincs mozgás, a súly pedig $\frac{\epsilon}{5}$-tel emelkedik meg. Tehát $1000\mathrm{\,N} \frac{\epsilon}{5}$ energiát kapott. Az egyenlet tehát: $F_A \epsilon = 1000\mathrm{\,N} \frac{\epsilon}{5}$. Ha kiosztjuk az $\epsilon$-t meg is vagyunk, hogy a jobboldali pilléren $F_B=$ 200 N erőt kell kifejtenünk.
Egy hidat elképzelhetünk így, mint különböző illesztési pontoknál felfüggesztett tárgyakat. Ha egy illesztési pontot elmozdítunk függőlegesen, a rendszer összesített helyzeti energiája nem változhat meg. Ha ez nem így lenne, akkor a súlyok elmozdulnának, és a híd összedőlne.
Mozgási energia
Ha egy tárgy mozog, akkor annak mozgási energiája van. Ez a mozgási energia a tömeggel egyenesen arányos. Tehát kétszer, háromszor nehezebb tárgy mozgási energiája azonos körülmények között kétszer, háromszor nagyobb. Viszont a sebességgel ez az energia négyzetesen arányos. Tehát kétszer, háromszor nagyobb sebesség négyszer, kilencszer nagyobb energiát jelent.
A mozgási energia képlete:
$$ E = \frac{mv^2}{2} $$
Itt $E$ a mozgási energia joule-ban, $m$ a test tömege kilóban, $v$ pedig a test sebessége méter/másodpercben. A sebesség nyilvánvalóan relatív. Így a mozgási energia is függ attól, hogy hogy honnét nézzük. De akárhonnét is nézzük, az energia összmennyisége állandó marad.
Jelenpillanatban 2 energiaformáról beszéltünk eddig: a helyzeti energiáról, és a mozgásiról. Tegyük fel, hogy van egy ingánk. Egy 1 kg tömegű testet rákötünk egy jó hosszú madzagra (mondjuk egy toronydaru kábelére). Majd kilendítjük az ingát úgy, hogy 20 méterre emelkedjen fel a golyó, majd a felfüggesztett golyót elengedjük. Milyen gyorsan fog áthaladni a test a holtponton?
Tehát 1 kg a test, súlya így 10 N. 20 m-re emeltük fel tehát ezzel 200 J helyzeti energiát adtunk neki. Amikor a test ezen a hosszú ingán átrepül a holtponton, ez a 200 J helyzeti energia teljesen átalakult mozgási energiává. A fenti képlet alapján kiszámolható, hogy ez a sebesség 20 méter/másodperc lesz. Vagy átszámítva 72 km/h-val repül át a holt ponton.
Ha ezt az 1 kg-os tárgyat 20 m magasból csak simán leejtjük, akkor milyen sebességgel csapódik majd a földbe? A válasz az, hogy teljesen mindegy, hogy ingáról van szó, vagy csak arról, hogy simán leejtjük: ha 20 méterről leejtjük, akkor mindenképp 200 J mozgási energiát kap, tehát 72 km/h-val csapódik a földbe. További érdekesség, hogyha ez a holtponti/becsapódási sebesség független a tömegtől. Hiszen a mozgási és a helyzeti energia is egyenesen arányos a tömeggel. Így kétszer, háromszor nagyobb tömegnél, kétszer háromszor nagyobb az energia. Viszont, amikor a sebességet számoljuk, akkor mindig leosztjuk a tömeget. Ezért teljesen mindegy, hogy az ingán 1 kiló vagy 100 kiló van-e a sebesség ugyanannyi.
A dolog érdekessége, hogy a budapesti metró menetsebessége 70 km/h. Építhetnénk úgy a metrót, hogy 20 méterrel a föld alatt haladjon, viszont az állomásai a felszínen lennének. Így induláskor csak simán lezuhog a 20 méter mélyen lévő alagútba és így minimális meghajtással tud felgyorsulni menetsebességre (72 km/h-ra). Majd, amikor jön a következő megálló, akkor megmássza újra a 20 méteres emelkedőt és így lassul le a megállóban való beálláshoz. Nem kell gyorsítani, és nem kell fékezni sem, megoldja a gravitáció (csak korrigálni kell). Csodálkozom azon, hogy miért nem építettek így metrót soha sem még...
Hőenergia
Ha megmozdítunk valamit, vagy elgurítunk valamit, az egy idő után meg is fog állni. Na hova lesz akkor az energia? Ilyenkor az történik, hogy a mozgási energia át lesz adva az atomoknak. Ha valami csúszik vagy gurul, akkor elkerülhetetlen, hogy a mozgási energia egy része áttevődjön az atomokra. Ezek az atomok mozgási energiát nyernek, majd elosztják azt egymás között: a tárgy felmelegszik. A víznek és a levegőnek van közegellenállása, ha mozog benne valami, akkor közeg lassítja. Itt is az történik, hogy a mozgási energiánk áthelyeződik az atomokra, és a gáz vagy folyadék, amiben a test mozog felmelegszik.
A hő az az energiaforma, amelybe minden más energiaforma különösen szeret átalakulni. Ha egyszer már össze-vissza mennek az atomok, akkor azokat nagyon nehéz lesz újra rávenni arra, hogy újra egyetemesen egyenes vonalban menjenek. Amíg a mozgási energia és a helyzeti energia teljes egészében képes hővé alakulni, addig a hő nem tud ezekké korlátlanul visszaalakulni.
A hő munkára fogható, miközben áramlik a melegebb helyről a hidegebbre. Így működik például a gőzmozdony és az összes belsőégésű motor. Viszont nem lehet felhasználni az összes átáramló hőt arra, hogy munkát végezzen (ez az ún. Carnot-hatásfok), csak egy részét, mivel valamennyi hőnek mindenképpen meg kell érkeznie végül a hidegebb területre.
Elektromos energia
Ha valahol sok energia kell, akkor csak oda kell húzni az elektromos vezetéket, és már lehet használni is. Amióta van elektromos energia, az energia irányítása még soha se volt ilyen egyszerű, mint most.
Helyzeti energiát úgy adtunk egy testnek, hogy a gravitációs mező ellenében felemeltük. Ha egy elektromos töltést mozgatunk egy elektromos mező ellenében, akkor annak elektromos helyzeti energiája lesz. Az elektromos potenciál esetén a tömeg szerepét átveszi az elektromos töltés, amelyet coulombban (C) mérünk. A magasság szerepét pedig átveszi a potenciál, amit pedig voltban (V) mérünk. Ahogy a helyzeti energiánál is mérhetjük a magasságot tetszőleges nulla ponttól, úgy a potenciált is mérhetjük tetszőleges nulla ponttól (tipikusan a nullvezeték potenciáljától). Ahogy a mechanikai helyzeti energia nullapontja is tetszőleges, úgy az elektromos helyzeti energiáé is. A generátorok, elemek és egyéb elektromos energiát adó eszközök úgy működnek, hogy a két kimenetük között elektromos potenciálkülönbséget hoznak létre.
Az elektromos töltések munkát végeznek, miközben a magasabb potenciálú területről az alacsony potenciálú területre mozognak. Tehát, ha van 1 C elektromos töltésünk és átmozgatjuk azt egy 300 V-os potenciálkülönbségen, akkor ez az elektromos töltés 300 J munkát fog végezni. És nem számít, hogy az a két pont amelyen a töltések átszállnak milyen messze van egymástól. Ha 300 V a potenciálkülönbség, és 1 C a töltés, akkor 300 J a munka.
Gyakorlatban az ember nem sokszor lát coulombot, inkább ampert (A) szokott látni. Az 1 A = 1 C/s annak az áramnak erőssége, amikor 1 C töltés megy át egy vezetéken 1 másodperc alatt. Ha több töltés megy át, akkor nagyobb az áramerősség. Ha coulombot nem is, de azért az amperórát (Ah) még lát az ember néha, ami az akkumulátorokban tárolt töltés mennyiségét jelenti. 1Ah = 3600 C.
Ha 300 V potenciálkülönbségen 1 A erősségű áram folyik, akkor ott minden másodpercben 300 J munka végződik. Az egységnyi idő alatt elvégzett munkának is van mértékegysége: a watt (W) = J/s. Ha 1 J munka kerül elvégzésre másodpercenként alatt, az 1W. Egy építőmunkás kb. 80 W teljesítménnyel üzemel, amikor dolgozik. Tehát, amikor az 1000 W-os hajszárítóval szárítjuk magunkat, akkor azt a hőt kb. 13 munkás tudná előállítani folyamatos munkával. És akkor végül még egy mértékegység. A villanyszámlát tipikusan kilowattóra (kWh) után szoktuk fizetni. 1 kWh = 3600000 J = 3,6 MJ, tehát elég nagy energia. Viszont 1 óráig járatod a hajszárítót és már el is fogyott. Ez nagyon sok energia egyébként, ennyi energiával egy 1 tonnás autót 360 m magasra lehetne emelni.
Sugárzás
Nem kifejezetten energiaforma ez, hanem inkább az energiaközlés egy módja. A tárgyaknak azért van hőmérséklete, mert bennük az atomok izegnek mozognak. Mivel az atomok elektromosan töltött részekből állnak, ezért a folytonos mozgásuk elektromágneses sugárzást kelt. Így minden test fokozatosan lehűl pusztán azért, mert sugározza szét a hőjét, még akkor is, hogyha eközben egyetlen atommal sem kerül kapcsolatba. Azonban nem csak sugároznak a tárgyak, hanem el is nyelik a sugárzást. Ha egy test több sugárzást nyel el, mint amennyit kisugároz, akkor felmelegszik, ha többet bocsát ki, mint amennyit elnyel, akkor lehűl. Minél melegebb egy tárgy, annál nagyobb teljesítménnyel sugároz. Így ha egy tárgyat nála melegebb tárgyakkal veszünk körbe, akkor több sugárzást fog elnyelni, mint amennyit kibocsát, tehát felmelegszik. Ha pedig egy tárgyat nála hidegebb tárgyakkal veszünk körbe, akkor több sugárzást fog kibocsátani, mint amennyi elnyel, így lassan lehűl.
Kémiai energia
A kémiai energia az az energia, amely az atomok elektronfelhőjében van. Ha két atom összekapcsolódik, akkor ennek egy része általában felszabadul. Ez nagy mennyiségű energiát jelent. Kémiai energia szabadul fel, amikor például elégetünk egy éghető anyagot. Vagy amikor egy robbanószer felrobban. Ha két atom összekapcsolódása energiafelszabadulással járt, akkor a szétválasztásához ugyanennyi energiát kell befektetnünk. Például a szén-dioxid szétszedéséhez és a szén felhasználásához a növényeknek napenergiára van szüksége.
Rugalmas energia
Ahhoz, hogy a szilárd anyagok megtartsák az alakjukat és ne folyjanak szét, kell egy erő, amely a deformációnak ellent áll. Ez a rugalmas erő. Kisebb-nagyobb mértékben minden szilárd anyag rugalmas. Egy tárgy rugalmas deformálásához munkát kell végeznünk, ez a munka deformálás mértékének a négyzetével arányos. Tehát ha van egy rúgónk, és kétszer, háromszor nagyobb mértékben nyújtjuk meg, akkor ehhez négyszer, kilencszer nagyobb munkát kell végeznünk. Minden anyagnak van 2 rugalmassági jellemzője. Az egyik a rugalmassági modulus, a másik pedig az elasztikus határ. Minél nagyobb a rugalmassági modulus, annál nehezebb az adott anyagot deformálni. Minél kisebb a rugalmassági modulus, annál könnyebb, annál rugalmasabbnak érezzük az adott anyagot. Az elasztikus határ pedig a deformálásnak az a határa, amelyen túl a tárgy maradandó alakváltozást szenved (vagy eltörik).
Nukleáris energia
Az előző részben írtam, hogy az atommagban a protonokat és a neutronokat (együttesen a nukleonokat) az erős kölcsönhatás tartja össze. Ha két nukleon túl közel kerül egymáshoz, akkor az erős kölcsönhatás munkát végez és a két nukleon összekapcsolódik. A munka eredményeképpen a nukleáris energia felszabadul mozgási energia és sugárzás formájában. Hatalmas energiákról van szó.
Azonban ahhoz, hogy összenyomjunk 2 protont, az kell, hogy először legyőzzük az elektromos taszítást, amely kettejük között fennáll. Tehát munkát kell végeznünk. Majd amint elég közel ért a 2 proton, az erős kölcsönhatás összecsattantja őket. És ezen folyamat során nagyobb energia szabadul fel, mint amennyit összenyomáshoz fel kellett használnunk. Azonban ez a 2 proton összekapcsolódva nagyon instabil, ezért gyakran nyomban szétesik. Viszont ritkább esetben az egyik proton átalakulhat neutronná, és így kapunk egy deutériumot, azaz nehéz hidrogént, amelyben 1 proton és 1 neutron van. A folyamat során 420 keV energia szabadul fel 1eV: elektronvolt, az az energia, amelyet 1db elektron végez miközben egy 1V-os potenciálkülönbségen repül át. Ez nagyon kis energia: $1,6\cdot10^{-19}$ J. . Természetes körülmények között 2 proton csak a csillagokban képes így egyesülni és deutériummá alakulni. Egy proton és neutron is egyesülhet, ott nem kell legyőzni a két proton közötti taszítóerőt, az eredmény pedig egy deutérium lesz, és egy erős 2,2 MeV-es gamma foton. Amikor két nukleon egyesül azt úgy mondjuk, hogy fúzionálnak. A folyamatot pedig fúziónak nevezzük.
Van a fúziónak egy olyan formája amely megfelelő szakértelemmel akár otthon is elvégezhető. Fémdobozban egy drótgömbre kell kapcsolni kb. 20kV-ot. Majd kiszivattyúzni a belőle az összes levegőt, és befújni egy kis deutériumot. Ha megfelelő a nyomás, akkor ködfény kisülés történik, és a deutérium atomok elveszítik az elektronjukat, és némelyik pár 20 keV-nyi energiával csapódik egymásnak majd. Ez elegendő energia lehet, hogy a két deutérium fuzionáljon. A folyamat során keletkezhet hidrogén-3 (1 proton, 2 neutron, „nagyon nehéz hidrogén”, másik nevén trícium, és radioaktív), illetve hélium-3 (2 proton, 1 neutron, stabil). Ezek kb. 1 MeV energiával repülnek el, miközben az extra proton vagy neutron, kb. 3 MeV energiával fog elrepülni. Az ilyen eszközt úgy hívják, hogy fúzor. A fúziót pedig a vákuumkamra körül elhelyezett neutrondetektorokkal lehet bizonyítani. Ez az eszköz csak arra jó, hogy elmondhassa az ember, hogy csinált fúziót. Energiatermelésre alkalmatlan. Viszont a gyakorlatban használható nagy energiájú neutronforrásként, amely egy gombnyomással ki-be kapcsolható.
Ha sikerülne fúziós erőművet építeni, akkor minden energiagondunk meg van oldva. Hidrogén bőségesen rendelkezésre áll a természetből (ellenben az uránnal, amelyből csak nagyon kevés van). Vannak különféle próbálkozások, hogy hogyan lehetne fúziós erőművet építeni. A kihívás az, hogy 100 millió fokos alacsony nyomású deutérium gázt kell a reaktortérben tartani úgy, hogy ne érjen hozzá a reaktor falához. A legtöbb reménnyel a sztellarátor típusú reaktorok kecsegtetnek. Egy ilyet nagyon nehéz megépíteni, mert rendkívül bonyolult számítások kellenek hozzá. Csak manapság sikerült kiszámolni, hogy milyennek kell lennie egy sztellarátornak, hogy működhessen. Egy sztellarátorban mágneses mezővel tartják össze a plazmát miközben áramoltatják körbe-körbe egy fura alakú tartályban. A tartály alakja és a mágneses mező miatt nem fog hozzáérni a falhoz a plazma.
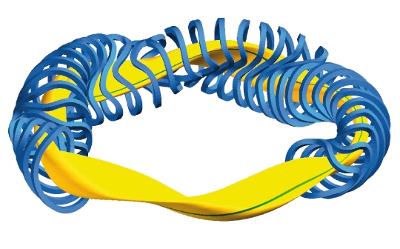
Ezekkel a furcsa alakú (kék) dróttekercsekkel lehet létrehozni azt a mágneses mezőt, amely a forró deutériumplazma faltól való távol tartásához szükséges. Nyilván az elülső néhány tekercs hiányzik, hogy jobban belelássunk. (forrás, szerző:Max-Planck Institut für Plasmaphysik, CC-BY-SA )
Na, ahhoz, hogy egy pozitív protont belenyomjunk egy atommagba először le kell győzni a pozitív atommag taszítóerejét. Tehát munkát kell végeznünk, és csak akkor csattanhat hozzá a proton az atommaghoz, amikor már elég közel került hozzá. A könnyű kémiai elemek esetén ez az összecsattanás nagyobb energiát szabadít fel, mint amennyi energia szükséges a két atommag összenyomásához. Viszont a 26-os rendszámú vastól kezdve (amiben már ugye 26 proton van), az újabb protonok atommagba nyomása több energiába kerül, mint amennyi a becsattanáskor felszabadul. A vas atommagja már túl pozitív, túl erősen taszítja az új protont. Így a nehéz elemek fúziója során már kevesebb energia szabadul fel, mint amennyi befektetésre kerül. Emiatt a csillagokban is csak addig működik a magfúzió, amíg el nem kezd a csillag vasat gyártani. Ha ez megtörténik, akkor a csillag összeomlik a saját súlya alatt, és a fúziót ezentúl a magra ráomló anyag helyzeti energiája táplálja. És ez csinál nagyon gyorsan vasnál nehezebb elemeket. Ez már a csillag életének a végén történik, amelynek az a vége, hogy a csillag a végén szupernóvaként felrobban, mert az összenyomódó magról a ráomló anyag visszapattan.
Az igazán nehéz (ólomnál nagyobb rendszámú) elemek már radioaktívak, azaz annyi proton van bennük, hogy azoknak az erős az egymásra gyakorolt elektromos taszítása már néha képes legyőzni az erős kölcsönhatást, és kivetni az atommag egyes darabjait. A folyamat során kirepülnek az atommag darabjai nagy sebességgel, tehát energia szabadul fel. Ezek a darabkák aztán esetleg más atommagokkal találkozva újabb szétesést eredményezhetnek, és láncreakciót indíthatnak el. Így működik az atombomba. Kontrollált körülmények között pedig az atomerőműben használják fel ezt az energiát.
A nukleáris energiát nyerhetjük fúzióból, és radioaktív bomlásból is. A fúzióból több energiát nyerhetünk (egységnyi üzemanyag tömegre vetítve), mint az urán bomlasztásából. Azonban még nem sikerült olyan erőművet építenünk, amely fúzióval működik. Ha egy sikerül, akkor az energiagondjaink lényegében egyszer s mindenkorra megoldódtak.
Tömeg energia
Talán az egyik legismertebb képlet az $E = mc^2$. Tehát a tömeget beszorozzuk a fénysebesség négyzetével. Ez a képlet azt jelenti, hogy minden anyagnak van energiája pusztán azért, mert tömege van. Vagy fordítva, azért van a dolgoknak tömege, mert energiája van. Ez hatalmas energiát jelent: 1 kg tömeg $9 \cdot 10^{16}$ J energiát jelent, ami nagyon sok. 2 kg tömegből naponta fedezhető lenne a világ teljes energiaszükséglete. Azonban ezt az energiát nem lehet csak úgy felszabadítani. De a fenti összefüggés használható arra, hogy megadjuk a magyarázatot arra, hogy egy hélium atom miért könnyebb, mint 2-2 proton és neutron külön-külön: az energia egy része eltávozott, amikor ezek az alkotórészek egyesültek a fúzió során.
Miért is marad meg az energia és egyéb dolgok?
A fizikusok gyakran beszélnek ún. szimmetriákról. De mi is az a szimmetria? A mindennapi életben tipikusan olyan dolgokra használjuk azt a szót, hogy szimmetrikus, amely tükrözve vagy forgatva önmagába megy át.
A szimmetria viszont jóval általánosabb dolog ennél. Tegyük fel, hogy van valamilyen rendszerünk. Csinálunk vele valamit. Ha ez a megváltoztatott rendszer valamilyen tekintetben nem különböztethető meg az eredetitől, akkor ott valamilyen szimmetria van. És ahol szimmetria van, ott valamilyen megmaradási törvény is kell, hogy legyen. Ez az ún. Noether-tétel. És ez az oka annak, hogy megmarad a lendület, a perdület, az energia, és még sok más is.
A fizikai jelenségek ma és holnap is ugyanolyan módon, megkülönböztethetetlenül történnek. Ez egy szimmetria, az időbeli eltolás szimmetriája. A hozzátartozó megmaradási törvény az energiamegmaradás törvénye.
Egy másik szimmetria a helyfüggetlenség. Teljesen mindegy, hogy itt vagy 100 méterrel arrébb ejtek-e le egy almát azonos magasságból. A két esetben a helyzeti energia és minden más ugyanaz, tehát megkülönböztethetetlen a kettő eset. Tehát ez is egy szimmetria. A helyfüggetlenség megmaradási törvénye a lendületmegmaradás törvénye: ha valamit meglökünk, az egyenes vonalban egyenletes sebességgel halad (amíg valami erő nem hat rá). És valóban egy eldobott tárgy vízszintes irányú lendülete megmarad. Azonban a függőleges irányú nem. Mert függőleges irányban változik a helyzeti energia, a testnek egyre több függőleges lendülete lesz, ahogy esik lefelé. Ezért a fentebb és a lentebb lévő alma megkülönböztethető. Függőleges irányban nincs szimmetria, így a függőleges lendület nem is marad meg, csak a vízszintes.
Egy másik szimmetria a helyzetfüggetlenség. Ha valami független az adott tárgy vagy kísérleti eszköz helyzetétől, akkor az is egy szimmetria. Például az alma fejjel lefelé és bármilyen helyzetben is ugyanúgy leesik. Semmi különbség nincs a helyzetek között. Ez is egy szimmetria. Az ehhez tartozó megmaradási törvény pedig a perdületmegmaradás törvénye: ha valamit megpörgetünk, az folyamatosan pörögni fog, amíg valamilyen forgatónyomaték meg nem változtatja a forgásállapotát. Persze az alma esése csak tökéletes vákuumban lenne független a helyzetétől. Hogyha feltételezzük, hogy van légellenállás, akkor az aerodinamikai tulajdonságok miatt számítani fog, hogy milyen helyzetben esik le az alma. Így a valóságos helyzetben a perdülete sem maradhat meg: ebből következik az, hogyha egy forgó almát ejtünk le, akkor a légellenállás valamilyen forgatónyomatékkal hat majd rá. És mi kijelenthetjük ezt, anélkül, hogy rendkívül bonyolult számításokat kellene elvégeznünk az alma aerodinamikáját illetően, csupán a szimmetriákra hagyatkozva.
Beszéltünk izolált rendszerek (például egy darab alma) szimmetriáiról. Viszont mi a helyzet az egész világgal? Ha időben előre tolnánk a világot minden ugyanúgy történne: az energia a világban megmarad. A másodpercek nincsenek felcímkézve. Ha az egész világot mindenestül arrébb tolnánk, nem jönnénk rá, hogy ilyen történt, minden ugyanúgy történne: a lendület megmarad. A tér pontjai sincsenek felcímkézve. Ha az egész világot mindenestül elforgatnánk, nem jönnénk rá, hogy a világ milyen helyzetben van: a perdület is megmarad világszinten.
Hasonlóan szimmetriák vannak a barion és a leptonszám megmaradásának a törvénye mögött is.
